
【题目】如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,垂足为F.
(1)求证:△ABC≌△ADE;(图1)
(2)求∠FAE的度数;(图1)
(3)如图2,延长CF到G点,使BF=GF,连接AG.求证:CD=CG;并猜想CD与2BF+DE的关系.

【答案】(1)证明见解析;(2)∠FAE=135°;(3)证明见解析.
【解析】
(1)根据题意和题目中的条件可以找出△ABC≌△ADE的条件;
(2)根据(1)中的结论和等腰直角三角形的定义可以得到∠FAE的度数;
(3)根据题意和三角形全等的知识,作出合适的辅助线即可证明结论成立.
(1)证明:∵∠BAD=∠CAE=90°,
∴∠BAC+∠CAD=90°,∠CAD+∠DAE=90°,
∴∠BAC=∠DAE,
在△BAC和△DAE中,
 ,
,
∴△BAC≌△DAE(SAS);
(2)解:∵∠CAE=90°,AC=AE,
∴∠E=45°,
由(1)知△BAC≌△DAE,
∴∠BCA=∠E=45°,
∵AF⊥BC,
∴∠CFA=90°,
∴∠CAF=45°,
∴∠FAE=∠FAC+∠CAE=45°+90°=135°;
(3)证明:∵AF⊥BG,
∴∠AFG=∠AFB=90°,
在△AFB和△AFG中,
 ,
,
∴△AFB≌△AFG(SAS),
∴AB=AG,∠ABF=∠G,
∵△BAC≌△DAE,
∴AB=AD,∠CBA=∠EDA,CB=ED,
∴AG=AD,∠ABF=∠CDA,
∴∠G=∠CDA,
在△CGA和△CDA中,
 ,
,
∴△CGA≌△CDA,
∴CG=CD,
∵CG=CB+BF+FG=CB+2BF=DE+2BF,
∴CD=2BF+DE.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点M的坐标为(3,﹣2),线段AB的位置如图所示,其中点A的坐标为(7,3),点B的坐标为(1,4).
(1)将线段AB平移可以得到线段MN,其中点A的对应点为M(3,﹣2),点B的对应点为N,则点N的坐标为 .
(2)在(1)的条件下,若点C的坐标为(4,0),请在图中描出点N并顺次连接BC,CM,MN,NB,然后求出四边形BCMN的面积S.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣(2m+1)+( ![]() m2﹣1).
m2﹣1).
(1)求证:不论m取什么实数,该二次函数图象与x轴总有两个交点;
(2)若该二次函数图象经过点(2m﹣2,﹣2m﹣1),求该二次函数的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
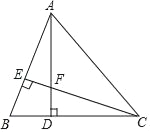
【题目】如图所示,在△ABC中,AD⊥BC于D,CE⊥AB于E,AD与CE交于点F,且AD=CD.
(1)求证:△ABD≌△CFD;
(2)已知BC=7,AD=5,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y= ![]() 的图象上.若点B在反比例函数y=
的图象上.若点B在反比例函数y= ![]() 的图象上,则k的值为 .
的图象上,则k的值为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
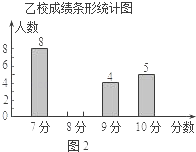
【题目】甲、乙两校参加区教育局举办的学生英语口语竞赛,两校参赛人数相等.比赛结束后,发现学生成绩分别为7分、8分、9分、10分(满分为10分).依据统计数据绘制了如下尚不完整的统计图表. 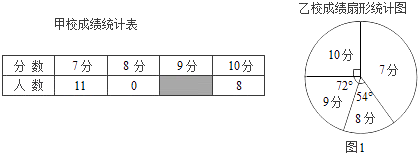
(1)在图1中,“7分”所在扇形的圆心角等于°.
(2)请你将图2的统计图补充完整;
(3)经计算,乙校的平均分是8.3分,中位数是8分,请写出甲校的平均分、中位数;并从平均分和中位数的角度分析哪个学校成绩较好.
(4)如果该教育局要组织8人的代表队参加市级团体赛,为便于管理,决定从这两所学校中的一所挑选参赛选手,请你分析,应选哪所学校?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列条件中,不能证明△ABC≌△DCB是 ( )

A. AB=DC,AC=DB B. AB=DC,∠ABC=∠DCB
C. DB=AC,∠DBC=∠ACB D. DC=AB,∠DBC=∠ACB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知长方形ABCD中,AD=6cm,AB=4cm,点E为AD的中点.若点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BC上由点B向点C运动.
(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△AEP与△BPQ是否全等,请说明理由,并直接写出此时线段PE和线段PQ的位置关系;
(2)若点Q的运动速度与点P的运动速度相等,运动时间为t秒,设△PEQ的面积为Scm2,请用t的代数式表示S;
(3)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△AEP与△BPQ全等?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com