
【题目】如图,△ABC中,AB=AC,将△ABC绕点A按逆时针方向旋转100°,得到△ADE,连接BD、CE. 求证:BD=CE.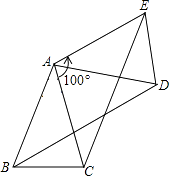
【答案】证明:∵△ABC绕点A按逆时针方向旋转100°得△ADE, ∴∠BAD=∠CAE=100°.
又∵AB=AC,
∴AB=AC=AD=AE.
在△ABD与△ACE中,
∵ 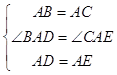 ,
,
∴△ABD≌△ACE(SAS).
∴BD=CE.
【解析】先根据图形旋转的性质得出∠BAD=∠CAE=100°,再由SAS定理得出△ABD≌△ACE,由全等三角形的性质即可得出结论.
【考点精析】本题主要考查了等腰三角形的性质和旋转的性质的相关知识点,需要掌握等腰三角形的两个底角相等(简称:等边对等角);①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了才能正确解答此题.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
【题目】如图(1)是某河上一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状.抛物线两端点与水面的距离都是1m,拱桥的跨度为10cm.桥洞与水面的最大距离是5m.桥洞两侧壁上各有一盏距离水面4m的景观灯.现把拱桥的截面图放在平面直角坐标系中,如图(2).求: 
(1)抛物线的解析式;
(2)两盏景观灯P1、P2之间的水平距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和爸爸周末步行去游泳馆游冰,爸爸先出发了一段时间后小明才出发,途中小明在离家1400米处的报亭休息了一段时间后继续按原来的速度前往游泳馆.两人离家的距离y(米)与小明所走时间x(分钟)之间的函数关系如图所示,请结合图象信息解答下列问题:
(1)小明出发_____分钟后第一次与爸爸相遇;
(2)分别求出爸爸离家的距离y1和小明到达报亭前离家的距离y2与时间x之间的函数关系式;
(3)求小明在报亭休息了多长时间遇到姗姗来迟的爸爸;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=2,∠BAC=45°,△AEF是由△ABC绕点A按逆时针方向旋转得到的,连接BE、CF相交于点D. 
(1)求证:BE=CF;
(2)当四边形ABDF为菱形时,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知一个多边形的内角和是它的外角和的 3 倍,求这个多边形的边数.
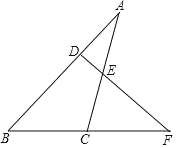
(2)如图,点F 是△ABC 的边 BC 延长线上一点.DF⊥AB,∠A=30°,∠F=40°,求∠ACF 的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
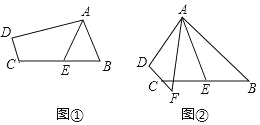
【题目】(1)如图①,在四边形ABCD中,AB∥DC,E是BC的中点,若AE是∠BAD的平分线,试探究AB,AD,DC之间的等量关系,证明你的结论;
(2)如图②,在四边形ABCD中,AB∥DC,AF与DC的延长线交于点F,E是BC的中点,若AE是∠BAF的平分线,试探究AB,AF,CF之间的等量关系,证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.

(1)求证:BG=CF.
(2)请你判断BE+CF与EF的大小关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农户种植一种经济作物,总用水量y(m3)与种植时间x(天)之间的函数关系如图所示.
(1)第20天的总用水量为 m3;
(2)当x≥20时,求y与x之间的函数表达式;
(3)种植时间为多少天时,总用水量达到7 000 m3.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学活动课上,小敏.小颖分别画了△ABC和△DEF , 尺寸如图 . 如果两个三角形的面积分别记作S△ABC.S△DEF , 那么它们的大小关系是( )
A.S△ABC>S△DEF
B.S△ABC<S△DEF
C.S△ABC=S△DEF
D.不能确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com