Question

13．小亮家今年种植的“翠香”猕猴桃喜获丰收，采摘上市20天全部销售完，小亮对销售情况进行跟踪记录，并将记录情况绘成图象，日销售量y（单位：千克）与上市时间x（单位：天）的函数关系如图1所示，猕猴桃价格z（单位：元/千克）与上市时间x（单位：天）的函数关系式如图2所示．

（1）求小亮家猕猴桃的日销售量y与上市时间x的函数解析式；
（2）试比较第10天与第12天的销售金额哪天多？请直接写出答案．

Answer 1

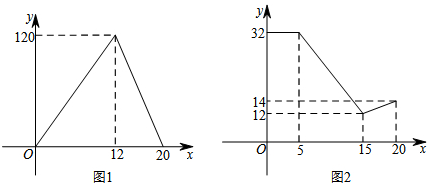
分析 （1）分别从0≤x≤12时与12＜x≤20去分析，利用待定系数法即可求得小亮家今年种植的“翠香”猕猴的日销售量y与上市时间x的函数解析式；
（2）先利用待定系数法求图2中当5＜x≤15时，猕猴桃价格z与上市时间x的函数解析式，再分别计算第10天与第12天的销售金额，作比较．

解答 解：（1）当0≤x≤12时，设日销售量与上市的时间的函数解析式为y=k₁x，
∵直线y=k₁x过点（12，120），
∴k₁=10，
∴函数解析式为y=10x，
当12＜x≤20，设日销售量与上市时间的函数解析式为y=k₂x+b，
∵点（12，120），（20，0）在y=k₂x+b的图象上，
∴$\left\{\begin{array}{l}{12{k}_{2}+b=120}\\{20{k}_{2}+b=0}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{{k}_{2}=-15}\\{b=300}\end{array}\right.$，
∴函数解析式为y=-15x+300，
∴小亮家猕猴桃的日销售量y与上市时间x的函数解析式：y=$\left\{\begin{array}{l}{10x（0≤x≤12）}\\{-15x+300（12＜x≤20）}\end{array}\right.$；
（2））∵第10天和第12天在第5天和第15天之间，
∴当5＜x≤15时，设猕猴桃价格z与上市时间x的函数解析式为z=mx+n，
∵点（5，32），（15，12）在z=mx+n的图象上，
∴$\left\{\begin{array}{l}{5m+n=32}\\{15m+n=12}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{m-2}\\{n=42}\end{array}\right.$，
∴函数解析式为z=-2x+42，
当x=10时，y=10×10=100，z=-2×10+42=22，
销售金额为：100×22=2200（元），
当x=12时，y=120，z=-2×12+42=18，
销售金额为：120×18=2160（元），
∵2200＞2160，
∴第10天的销售金额多．

点评 此题考查了一次函数的应用．此题难度适中，解题的关键是理解题意，利用待定系数法求得函数解析式，注意数形结合思想与函数思想的应用．