
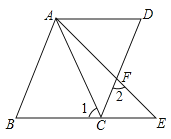
【题目】已知AD∥BE,∠B=∠D.
(1)求证:AB∥CD;
(2)若∠1=∠2=60°,∠BAC=3∠EAC,求∠DCE的度数.
【答案】(1)见解析;(2)75°
【解析】
(1)根据平行线的性质和判定解答即可;
(2)根据平行线的性质得到∠BAC+∠CAE=60°,设∠CAE=x,∠DAE=y,根据题意得到二元一次方程组求出x,y即可求解.
(1)∵AD∥BE,
∴∠D=∠DCE,
∵∠B=∠D,
∴∠DCE=∠B,
∴AB∥CD,
(2)∵AD∥BE,∠1=60°,
∴∠CAE+∠DAE=60°,
∵AB∥CD,∠2=60°,
∴∠BAC+∠CAE=60°,
∵∠BAC=3∠EAC,
设∠CAE=x,∠DAE=y,
可得:![]() ,
,
解得:![]() ,
,
即∠CAE=15°,∠DAE=45°,
∴∠D=180°60°45°=75°,
∴∠DCE=75°.


科目:初中数学 来源: 题型:
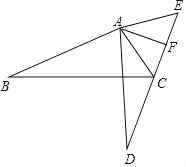
【题目】如图,∠BAD=∠CAE,AB=AD,AC=AE.且E,F,C,D在同一直线上.
(1)求证:△ABC≌△ADE;
(2)若∠B=30°,∠BAC=100°,点F是CE的中点,连结AF,求∠FAE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边△ABC所在平面内找出一个点,使它与三角形中的任意两个顶点所组成的三角形都是等腰三角形。这样的点一共有( )
A. 1个 B. 4个 C. 7个 D. 10个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明想了解全校3000名同学对新闻、体育、音乐、娱乐、戏曲五类电视节目的喜爱况,从中抽取了一部分同学进行了一次抽样调查,利用所得数据绘制成下面的统计图:根据图中所给信息,全校喜欢娱乐类节目的学生大约有( )人.

A. 1080 B. 900 C. 600 D. 108
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,点E,F分别是边BC,AB上的点,且CE=BF,连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC.

(1)请判断:FG与CE的数量关系是__________,位置关系是__________;
(2)如图2,若点E、F分别是CB、BA延长线上的点,其它条件不变,(1)中结论是否仍然成立?请出判断判断并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为更好地推进太原市生活垃圾分类工作,改善城市生态环境,2019年12月17日,太原市政府召开了太原市生活垃圾分类推进会,意味着太原垃圾分类战役的全面打响.某小区准备购买A、B两种型号的垃圾箱,通过市场调研得知:购买3个A型垃圾箱和2个B型垃圾箱共需540元,购买2个A型垃圾箱比购买3个B型垃圾箱少用160元.
(1)求每个A型垃圾箱和B型垃圾箱各多少元?
(2)该小区物业计划用不多于2100元的资金购买A、B两种型号的垃圾箱共20个,则该小区最多可以购买B型垃圾箱多少个?
(3)在(2)的条件下,要求至少购买3个B型垃圾箱,请设计出最省钱的购买方案,并求出最少购买费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将九年级部分男生掷实心球的成绩进行整理,分成5个小组(x表示成绩,单位:米).A组:5.25≤x<6.25;B组:6.25≤x<7.25;C组:7.25≤x<8.25;D组:8.25≤x<9.25;E组:9.25≤x<10.25,并绘制出扇形统计图和频数分布直方图(不完整).规定x≥6.25为合格,x≥9.25为优秀.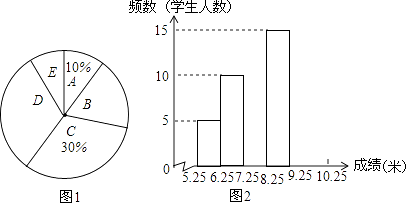
(1)这部分男生有多少人?其中成绩合格的有多少人?
(2)这部分男生成绩的中位数落在哪一组?扇形统计图中D组对应的圆心角是多少度?
(3)要从成绩优秀的学生中,随机选出2人介绍经验,已知甲、乙两位同学的成绩均为优秀,求他俩至少有1人被选中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com