
【题目】如图1,在正方形ABCD中,点E,F分别是边BC,AB上的点,且CE=BF,连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC.

(1)请判断:FG与CE的数量关系是__________,位置关系是__________;
(2)如图2,若点E、F分别是CB、BA延长线上的点,其它条件不变,(1)中结论是否仍然成立?请出判断判断并给予证明.
【答案】(1) FG=CE,FG∥CE;(2)成立,理由见解析.
【解析】
(1)结论:FG=CE,FG∥CE,如图1中,设DE与CF交于点M,首先证明△CBF≌△DCE,推出DE⊥CF,再证明四边形EGFC是平行四边形即可;
(2)结论仍然成立,如图2中,设DE与CF交于点M,首先证明△CBF≌△DCE,推出DE⊥CF,再证明四边形EGFC是平行四边形即可.
(1)结论:FG=CE,FG∥CE.
理由:如图1中,设DE与CF交于点M,
∵四边形ABCD是正方形,
∴BC=CD,∠ABC=∠DCE=90°,
在△CBF和△DCE中, ,
,
∴△CBF≌△DCE,
∴∠BCF=∠CDE,CF=DE,
∵∠BCF+∠DCM=90°,
∴∠CDE+∠DCM=90°,
∴∠CMD=90°,
∴CF⊥DE,
∵GE⊥DE,
∴EG∥CF,
∵EG=DE,CF=DE,
∴EG=CF,
∴四边形EGFC是平行四边形.
∴GF=EC,
∴GF=EC,GF∥EC.
故答案为FG=CE,FG∥CE;
(2)结论仍然成立.
理由:如图2中,设DE与CF交于点M,
∵四边形ABCD是正方形,
∴BC=CD,∠ABC=∠DCE=90°,
在△CBF和△DCE中, ,
,
∴△CBF≌△DCE,
∴∠BCF=∠CDE,CF=DE,
∵∠BCF+∠DCM=90°,
∴∠CDE+∠DCM=90°,
∴∠CMD=90°,
∴CF⊥DE,
∵GE⊥DE,
∴EG∥CF,
∵EG=DE,CF=DE,
∴EG=CF,
∴四边形EGFC是平行四边形.
∴GF=EC,
∴GF=EC,GF∥EC.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:
【题目】随着“互联网+”时代的到来,一种新型打车方式受到大众欢迎,该打车方式的总费用由里程费和耗时费组成,其中里程费按![]() 元/公里计算,耗时费按
元/公里计算,耗时费按![]() 元/分钟计算(总费用不足
元/分钟计算(总费用不足![]() 元按
元按![]() 元计价).小敏、小刚两人用该打车方式出行,按上述计价规则,其行驶里程数、耗时以及打车总费用如下表:
元计价).小敏、小刚两人用该打车方式出行,按上述计价规则,其行驶里程数、耗时以及打车总费用如下表:
里程数 | 耗时 | 车费(元) | |
小敏 |
|
|
|
小刚 |
|
|
|
![]() 求
求![]() 的值;
的值;
![]() 若小华也用该打车方式打车,平均车速为
若小华也用该打车方式打车,平均车速为![]() 公里/时,行驶了
公里/时,行驶了![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学学生会为了考察该校1800名学生参加课外体育活动的情况,采取抽样调查的方法从“篮球、排球、乒乓球、足球及其他”等五个方面调查了若干名学生的兴趣爱好(每人只能选其中一项),并将调查结果绘制成如下两幅不完整的统计图,请根据图中提供的信息,下列判断:①本次抽样调查的样本容量是60;②在扇形统计图中,“其他”部分所对应的圆心角是60°;③该校学生中喜欢“乒乓球”的人数约为450人;④若被抽查的男女学生数相同,其中喜欢球类的男生占喜欢球类人数的56.25%,则被抽查的学生中,喜欢“其他”类的女生数为9人.其中正确的判断是( )

A. 只有①②③B. 只有①②④C. 只有①③④D. 只有③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,随着我国的科学技术的迅猛发展,很多行业已经由“中国制造”升级为“中国创造”,高铁事业是“中国创造”的典范,一般的高铁包括G字头的高速动车组以及D字头的动车组.由大连到北京的G377的平均速度是D31的平均速度的1.2倍,行驶相同的路程1500千米,G377少用1个小时.
(1)求D31的平均速度.
(2)若以“速度与票价的比值”定义这两种列车的性价比,人们出行都喜欢选择性价比高的方式.现阶段D31票价为266元/张,G377票价为400元/张,如果你有机会给有关部门提一个合理化建议,使G377的性价比达到D31的性价比,你如何建议,为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
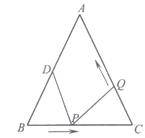
【题目】如图,已知在△ABC中,AB=AC=10cm,BC=8cm,D为AB中点,设点P在线段BC上以3cm/秒的速度由B点向C点运动,点Q在线段CA上由C点向A点运动.
(1)若Q点运动的速度与P点相同,且点P,Q同时出发,经过1秒钟后△BPD与△CQP是否全等,并说明理由;
(2)若点P,Q同时出发,但运动的速度不相同,当Q点的运动速度为多少时,能在运动过程中有△BPD与△CQP全等?
(3)若点Q以(2)中的速度从点C出发,点P以原来的速度从点B同时出发,都是逆时针沿△ABC的三边上运动,经过多少时间点P与点Q第一次在△ABC的哪条边上相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校利用二维码进行学生学号统一编排.黑色小正方形表示1,白色小正方形表示0,将每一行数字从左到右依次记为a,b,c,d,那么利用公式![]() 计算出每一行的数据.第一行表示年级,第二行表示班级,第三行表示班级学号的十位数,第四行表示班级学号的个位数.如图1所示,第一行数字从左往右依次是1,0,0,1,则表示的数据为1×23+0×22+0×21+1=9,计作09,第二行数字从左往右依次是1,0,1,0,则表示的数据为1×23+0×22+1×21=10,计作10,以此类推,图1代表的统一学号为091034,表示9年级10班34号.小明所对应的二维码如图2所示,则他的统一学号为_______.
计算出每一行的数据.第一行表示年级,第二行表示班级,第三行表示班级学号的十位数,第四行表示班级学号的个位数.如图1所示,第一行数字从左往右依次是1,0,0,1,则表示的数据为1×23+0×22+0×21+1=9,计作09,第二行数字从左往右依次是1,0,1,0,则表示的数据为1×23+0×22+1×21=10,计作10,以此类推,图1代表的统一学号为091034,表示9年级10班34号.小明所对应的二维码如图2所示,则他的统一学号为_______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com