
【题目】随着“互联网+”时代的到来,一种新型打车方式受到大众欢迎,该打车方式的总费用由里程费和耗时费组成,其中里程费按![]() 元/公里计算,耗时费按
元/公里计算,耗时费按![]() 元/分钟计算(总费用不足
元/分钟计算(总费用不足![]() 元按
元按![]() 元计价).小敏、小刚两人用该打车方式出行,按上述计价规则,其行驶里程数、耗时以及打车总费用如下表:
元计价).小敏、小刚两人用该打车方式出行,按上述计价规则,其行驶里程数、耗时以及打车总费用如下表:
里程数 | 耗时 | 车费(元) | |
小敏 |
|
|
|
小刚 |
|
|
|
![]() 求
求![]() 的值;
的值;
![]() 若小华也用该打车方式打车,平均车速为
若小华也用该打车方式打车,平均车速为![]() 公里/时,行驶了
公里/时,行驶了![]()
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x>40),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元,并把结果填写在表格中: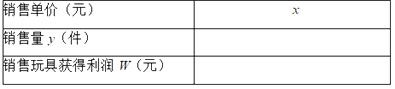
(2)在(1)条件下,若商场获得了10000元销售利润,求该玩具销售单价x应定为多少元.
(3)在(1)条件下,若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于540件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点P与点Q不重合,以点P为圆心作经过Q的圆,则称该圆为点P、Q的“相关圆” 
(1)已知点P的坐标为(2,0) ①若点Q的坐标为(0,1),求点P、Q的“相关圆”的面积;
②若点Q的坐标为(3,n),且点P、Q的“相关圆”的半径为 ![]() ,求n的值;
,求n的值;
(2)已知△ABC为等边三角形,点A和点B的坐标分别为(﹣ ![]() ,0)、(
,0)、( ![]() ,0),点C在y轴正半轴上,若点P、Q的“相关圆”恰好是△ABC的内切圆且点Q在直线y=2x上,求点Q的坐标.
,0),点C在y轴正半轴上,若点P、Q的“相关圆”恰好是△ABC的内切圆且点Q在直线y=2x上,求点Q的坐标.
(3)已知△ABC三个顶点的坐标为:A(﹣3,0)、B( ![]() ,0),C(0,4),点P的坐标为(0,
,0),C(0,4),点P的坐标为(0, ![]() ),点Q的坐标为(m,
),点Q的坐标为(m, ![]() ),若点P、Q的“相关圆”与△ABC的三边中至少一边存在公共点,直接写出m的取值范围.
),若点P、Q的“相关圆”与△ABC的三边中至少一边存在公共点,直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB⊥BC,AB∥DC,AB,BC,CD分别为2,2,2![]() +2,则∠BAD的度数等于( )
+2,则∠BAD的度数等于( )

A. 120° B. 135° C. 150° D. 以上都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AH是⊙O的直径,矩形ABCD交⊙O于点E,连接AE,将矩形ABCD沿AE折叠,点B落在CD边上的点F处,画直线EF. 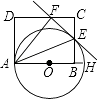
(1)求证:直线EF是⊙O的切线.
(2)若CD=10,EB=5,求⊙O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边△ABC所在平面内找出一个点,使它与三角形中的任意两个顶点所组成的三角形都是等腰三角形。这样的点一共有( )
A. 1个 B. 4个 C. 7个 D. 10个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,点E,F分别是边BC,AB上的点,且CE=BF,连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC.

(1)请判断:FG与CE的数量关系是__________,位置关系是__________;
(2)如图2,若点E、F分别是CB、BA延长线上的点,其它条件不变,(1)中结论是否仍然成立?请出判断判断并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次期中考试中,甲、乙、丙、丁、戊五位同学的数学、英语成绩等有关信息如下表所示(单位:分):
(1)求这五位同学在本次考试中数学成绩的平均分和英语成绩的标准差;
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,标准分的计算公式:标准分=(个人成绩-平均成绩)÷成绩标准差.
从标准分看,标准分大的考试成绩更好,请问甲同学在本次考试中,数学与英语哪个学科考得更好?
甲 | 乙 | 丙 | 丁 | 戊 | 平均分 | 标准差 | |
数学 | 71 | 72 | 69 | 68 | 70 | ||
英语 | 88 | 82 | 94 | 85 | 76 | 85 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com