
【题目】如图,AH是⊙O的直径,矩形ABCD交⊙O于点E,连接AE,将矩形ABCD沿AE折叠,点B落在CD边上的点F处,画直线EF. 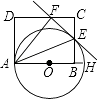
(1)求证:直线EF是⊙O的切线.
(2)若CD=10,EB=5,求⊙O的直径.
【答案】
(1)证明:
如图,连接OE,
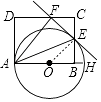
∵OA=OE,
∴∠EAO=∠AEO,
由折叠可得∠EAO=∠FAE,
∴∠FAE=∠AEO,
∴AF∥OE,
∴∠AFE+∠OEF=180°,
在矩形ABCD中,∠ABC=90°,
由折叠可知∠AFE=∠ABC=90°,
∴∠OEF=90°,
∴OE⊥EF,且点E在圆上,OE为半径,
∴EF是⊙O的切线
(2)解:∵四边形ABCD是矩形,CD=10,
∴AB=CD=10,∠ABE=90°,
设OA=OE=x,则OB=10﹣x,
在Rt△OBE中,∠OBE=90°,EB=5,
由勾股定理可得OB2+BE2=OE2,
∴(10﹣x)2+52=x2,解得x= ![]() ,
,
∴AH=2x= ![]() ,
,
∴⊙O的直径为 ![]()
【解析】(1)连接OE,由折叠的性质结合条件可证得OE∥AF,再由条件可得AF⊥EF,则可证得结论;(2)可设OA=OE=x,则OB=10﹣x,在Rt△OBE中,可求得x的值,进一步可求得⊙O的直径.
【考点精析】本题主要考查了矩形的性质和翻折变换(折叠问题)的相关知识点,需要掌握矩形的四个角都是直角,矩形的对角线相等;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能正确解答此题.


 灵星计算小达人系列答案
灵星计算小达人系列答案科目:初中数学 来源: 题型:
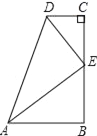
【题目】在数学活动课上,小明提出这样一个问题:如图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,则∠EAB的度数是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店分两次购进![]() 、
、![]() 两种商品进行销售,两次购进同一种商品的进价相同,具体情况如下表所示:
两种商品进行销售,两次购进同一种商品的进价相同,具体情况如下表所示:
购进数量(件) | 购进所需费用(元) | ||
|
| ||
第一次 | 30 | 40 | 3800 |
第二次 | 40 | 30 | 3200 |
(1)求![]() 、
、![]() 两种商品每件的进价分别是多少元?
两种商品每件的进价分别是多少元?
(2)商场决定![]() 种商品以每件30元出售,
种商品以每件30元出售,![]() 种商品以每件100元出售.为满足市场需求,需购进
种商品以每件100元出售.为满足市场需求,需购进![]() 、
、![]() 两种商品共1000件,且
两种商品共1000件,且![]() 种商品的数量不少于
种商品的数量不少于![]() 种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.
种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
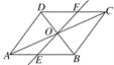
【题目】如图,在平行四边形ABCD中,对角线AC,BD交于点O,经过点O的直线交AB于E,交CD于F,AB=4,AD=3,OF=1.3.求四边形BCFE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形ABCD的四个顶点分别在格点上.
(1)画出四边形ABCD关于x轴对称的图形A′B′C′D′.
(2)将四边形ABCD向右平移得到四边形A″B″C″D″,使得△BB′B″为等腰直角三角形,画出四边形A″B″C″D″,并写出点C″的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着“互联网+”时代的到来,一种新型打车方式受到大众欢迎,该打车方式的总费用由里程费和耗时费组成,其中里程费按![]() 元/公里计算,耗时费按
元/公里计算,耗时费按![]() 元/分钟计算(总费用不足
元/分钟计算(总费用不足![]() 元按
元按![]() 元计价).小敏、小刚两人用该打车方式出行,按上述计价规则,其行驶里程数、耗时以及打车总费用如下表:
元计价).小敏、小刚两人用该打车方式出行,按上述计价规则,其行驶里程数、耗时以及打车总费用如下表:
里程数 | 耗时 | 车费(元) | |
小敏 |
|
|
|
小刚 |
|
|
|
![]() 求
求![]() 的值;
的值;
![]() 若小华也用该打车方式打车,平均车速为
若小华也用该打车方式打车,平均车速为![]() 公里/时,行驶了
公里/时,行驶了![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
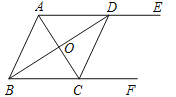
【题目】如图,AE∥BF,AC平分∠BAE,且交BF于点C,BD平分∠ABF,且交AE于点D,AC与BD相交于点O,连接CD
(1)求∠AOD的度数;
(2)求证:四边形ABCD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学学生会为了考察该校1800名学生参加课外体育活动的情况,采取抽样调查的方法从“篮球、排球、乒乓球、足球及其他”等五个方面调查了若干名学生的兴趣爱好(每人只能选其中一项),并将调查结果绘制成如下两幅不完整的统计图,请根据图中提供的信息,下列判断:①本次抽样调查的样本容量是60;②在扇形统计图中,“其他”部分所对应的圆心角是60°;③该校学生中喜欢“乒乓球”的人数约为450人;④若被抽查的男女学生数相同,其中喜欢球类的男生占喜欢球类人数的56.25%,则被抽查的学生中,喜欢“其他”类的女生数为9人.其中正确的判断是( )

A. 只有①②③B. 只有①②④C. 只有①③④D. 只有③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于二次函数y=x2-3x+2和一次函数y=-2x+4,把y=t(x2-3x+2)+(1-t)(-2x+4)称为这两个函数的“再生二次函数”,其中t是不为零的实数,其图象记作抛物线E.
现有点A(2,0)和抛物线E上的点B(-1,n),请完成下列任务:
(1)【尝试】
①当t=2时,抛物线E的顶点坐标是.
②点A抛物线E上;(填“在”或“不在”),
③n=.
(2)【发现】通过②和③的演算可知,对于t取任何不为零的实数,抛物线E总过定点,这个定点的坐标是.
(3)【应用1】二次函数y=-3x2+5x+2是二次函数y=x2-3x+2和一次函数y=-2x+4的一个“再生二次函数”吗?如果是,求出t的值;如果不是,说明理由.
(4)【应用2】以AB为一边作矩形ABCD,使得其中一个顶点落在y轴上,若抛物线E经过点A、B、C,求出所有符合条件的t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com