
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЃЌЕуPгыЕуQВЛжиКЯЃЌвдЕуPЮЊдВаФзїОЙ§QЕФдВЃЌдђГЦИУдВЮЊЕуPЁЂQЕФЁАЯрЙидВЁБ 
ЃЈ1ЃЉвбжЊЕуPЕФзјБъЮЊЃЈ2ЃЌ0ЃЉ ЂйШєЕуQЕФзјБъЮЊЃЈ0ЃЌ1ЃЉЃЌЧѓЕуPЁЂQЕФЁАЯрЙидВЁБЕФУцЛ§ЃЛ
ЂкШєЕуQЕФзјБъЮЊЃЈ3ЃЌnЃЉЃЌЧвЕуPЁЂQЕФЁАЯрЙидВЁБЕФАыОЖЮЊ ![]() ЃЌЧѓnЕФжЕЃЛ
ЃЌЧѓnЕФжЕЃЛ
ЃЈ2ЃЉвбжЊЁїABCЮЊЕШБпШ§НЧаЮЃЌЕуAКЭЕуBЕФзјБъЗжБ№ЮЊЃЈЉ ![]() ЃЌ0ЃЉЁЂЃЈ
ЃЌ0ЃЉЁЂЃЈ ![]() ЃЌ0ЃЉЃЌЕуCдкyжсе§АыжсЩЯЃЌШєЕуPЁЂQЕФЁАЯрЙидВЁБЧЁКУЪЧЁїABCЕФФкЧадВЧвЕуQдкжБЯпy=2xЩЯЃЌЧѓЕуQЕФзјБъЃЎ
ЃЌ0ЃЉЃЌЕуCдкyжсе§АыжсЩЯЃЌШєЕуPЁЂQЕФЁАЯрЙидВЁБЧЁКУЪЧЁїABCЕФФкЧадВЧвЕуQдкжБЯпy=2xЩЯЃЌЧѓЕуQЕФзјБъЃЎ
ЃЈ3ЃЉвбжЊЁїABCШ§ИіЖЅЕуЕФзјБъЮЊЃКAЃЈЉ3ЃЌ0ЃЉЁЂBЃЈ ![]() ЃЌ0ЃЉЃЌCЃЈ0ЃЌ4ЃЉЃЌЕуPЕФзјБъЮЊЃЈ0ЃЌ
ЃЌ0ЃЉЃЌCЃЈ0ЃЌ4ЃЉЃЌЕуPЕФзјБъЮЊЃЈ0ЃЌ ![]() ЃЉЃЌЕуQЕФзјБъЮЊЃЈmЃЌ
ЃЉЃЌЕуQЕФзјБъЮЊЃЈmЃЌ ![]() ЃЉЃЌШєЕуPЁЂQЕФЁАЯрЙидВЁБгыЁїABCЕФШ§БпжажСЩйвЛБпДцдкЙЋЙВЕуЃЌжБНгаДГіmЕФШЁжЕЗЖЮЇЃЎ
ЃЉЃЌШєЕуPЁЂQЕФЁАЯрЙидВЁБгыЁїABCЕФШ§БпжажСЩйвЛБпДцдкЙЋЙВЕуЃЌжБНгаДГіmЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁП
ЃЈ1ЃЉНтЃКЂйЁпPQ= ![]() =
= ![]() =
= ![]() ЃЌ
ЃЌ
ЁрS=Іаr2=5ІаЃЎ
ЂкЙ§ЕуQзїQHЁЭxжсгкHЃЎ

ЁпHQ= ![]() =2ЃЌ
=2ЃЌ
ЁрQЕузјБъЮЊЃЈ3ЃЌ2ЃЉЛђЃЈ3ЃЌЉ2ЃЉЃЎ
Ёрn=2ЛђЉ2
ЃЈ2ЃЉНтЃКШчЭМЃЌ
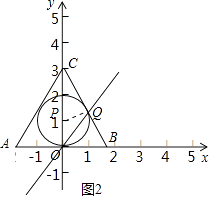
дкRtЁїOACжаЃЌЁЯACO=30ЁуЃЌ
ЁрOC= ![]() OA=3ЃЌ
OA=3ЃЌ
ЁрCЕузјБъЮЊЃЈ0ЃЌ3ЃЉЃЌ
ЁрЁїABCЕФФкЧадВЕФдВаФЕФзјБъЮЊЃЈ0ЃЌ1ЃЉЃЌАыОЖЮЊ1ЃЌ
ЁрPЃЈ0ЃЌ1ЃЉЃЌ
ЩшQЃЈxЃЌ2xЃЉЃЌдђгаx2+ЃЈ2xЉ1ЃЉ2=1ЃЌ
НтЕУx= ![]() ЃЌ
ЃЌ
ЁрQЃЈ ![]() ЃЌ
ЃЌ ![]() ЃЉ
ЃЉ
ЃЈ3ЃЉНтЃКШчЭМ3жаЃЌ

ЂйЕБЯрЙидВгыACЁЂABЯрЧаЪБАыОЖгазюаЁжЕ ![]() ЃЎ
ЃЎ
ЂкЕБЯрЙидВОЙ§ЕуBЪБЃЌАыОЖгазюДѓжЕ ![]() ЃЌ
ЃЌ
ЁрЉ ![]() ЁмmЁмЉ
ЁмmЁмЉ ![]() ЃЌ
ЃЌ ![]() ЁмmЁм
ЁмmЁм ![]()
ЁОНтЮіЁПЃЈ1ЃЉЂйИљОнPQ= ![]() =
= ![]() =
= ![]() ЃЌЧѓГіЁбPЕФАыОЖМДПЩНтОіЮЪЬтЃЛЂкЙ§ЕуQзїQHЁЭxжсгкHЃЎРћгУЙДЙЩЖЈРэЧѓГіQHЕФжЕЃЌМДПЩНтОіЮЪЬтЃЛЃЈ2ЃЉдкRtЁїOACжаЃЌЁЯACO=30ЁуЃЌПЩЕУOC=
ЃЌЧѓГіЁбPЕФАыОЖМДПЩНтОіЮЪЬтЃЛЂкЙ§ЕуQзїQHЁЭxжсгкHЃЎРћгУЙДЙЩЖЈРэЧѓГіQHЕФжЕЃЌМДПЩНтОіЮЪЬтЃЛЃЈ2ЃЉдкRtЁїOACжаЃЌЁЯACO=30ЁуЃЌПЩЕУOC= ![]() OA=3ЃЌЭЦГіCЕузјБъЮЊЃЈ0ЃЌ3ЃЉЃЌЭЦГіЁїABCЕФФкЧадВЕФдВаФЕФзјБъЮЊЃЈ0ЃЌ1ЃЉЃЌАыОЖЮЊ1ЃЌЭЦГіPЃЈ0ЃЌ1ЃЉЃЌЩшQЃЈxЃЌ2xЃЉЃЌдђгаx2+ЃЈ2xЉ1ЃЉ2=1ЃЌЧѓГіxМДПЩЃЛЃЈ3ЃЉЂйЕБЯрЙидВгыACЁЂABЯрЧаЪБЃЌПЩЕУАыОЖгазюаЁжЕ
OA=3ЃЌЭЦГіCЕузјБъЮЊЃЈ0ЃЌ3ЃЉЃЌЭЦГіЁїABCЕФФкЧадВЕФдВаФЕФзјБъЮЊЃЈ0ЃЌ1ЃЉЃЌАыОЖЮЊ1ЃЌЭЦГіPЃЈ0ЃЌ1ЃЉЃЌЩшQЃЈxЃЌ2xЃЉЃЌдђгаx2+ЃЈ2xЉ1ЃЉ2=1ЃЌЧѓГіxМДПЩЃЛЃЈ3ЃЉЂйЕБЯрЙидВгыACЁЂABЯрЧаЪБЃЌПЩЕУАыОЖгазюаЁжЕ ![]() ЃЎЂкЕБЯрЙидВОЙ§ЕуBЪБЃЌПЩЕУАыОЖзюДѓжЕ
ЃЎЂкЕБЯрЙидВОЙ§ЕуBЪБЃЌПЩЕУАыОЖзюДѓжЕ ![]() ЃЌгЩДЫМДПЩНтОіЮЪЬтЃЛ
ЃЌгЩДЫМДПЩНтОіЮЪЬтЃЛ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊжБЯпACЕФБэДяЪНЮЊyЃН![]() xЃЋ8ЃЌЕуPДгЕуAПЊЪМбиAOЯђЕуOвд1ИіЕЅЮЛ/sЕФЫйЖШвЦЖЏЃЌЕуQДгЕуOПЊЪМбиOCЯђЕуCвд2ИіЕЅЮЛ/sЕФЫйЖШвЦЖЏЃЎШчЙћPЃЌQСНЕуЗжБ№ДгЕуAЃЌOЭЌЪБГіЗЂЃЌОЙ§МИУыФмЪЙЁїPQOЕФУцЛ§ЮЊ8ИіЦНЗНЕЅЮЛЃП
xЃЋ8ЃЌЕуPДгЕуAПЊЪМбиAOЯђЕуOвд1ИіЕЅЮЛ/sЕФЫйЖШвЦЖЏЃЌЕуQДгЕуOПЊЪМбиOCЯђЕуCвд2ИіЕЅЮЛ/sЕФЫйЖШвЦЖЏЃЎШчЙћPЃЌQСНЕуЗжБ№ДгЕуAЃЌOЭЌЪБГіЗЂЃЌОЙ§МИУыФмЪЙЁїPQOЕФУцЛ§ЮЊ8ИіЦНЗНЕЅЮЛЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯпОЙ§ЕуЃЈ4ЃЌ3ЃЉЃЌЧвЕБ ![]() ЪБЃЌ
ЪБЃЌ ![]() газюаЁжЕ
газюаЁжЕ ![]() .
.
ЃЈ1ЃЉЧѓетЬѕХзЮяЯпЕФНтЮіЪН.
ЃЈ2ЃЉаДГі ![]() Ыц
Ыц ![]() ЕФдіДѓЖјМѕаЁЕФздБфСП
ЕФдіДѓЖјМѕаЁЕФздБфСП ![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЁїABCжаЃЌBA=BCЃЌBEЦНЗжЁЯABCЃЌCDЁЭBDЃЌЧвCD=BDЃЎ
ЃЈ1ЃЉЧѓжЄЃКBF=ACЃЛ
ЃЈ2ЃЉШєAD=![]() ЃЌЧѓCFЕФГЄЃЎ
ЃЌЧѓCFЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩЬЕъЗжСНДЮЙКНј![]() ЁЂ
ЁЂ![]() СНжжЩЬЦЗНјааЯњЪлЃЌСНДЮЙКНјЭЌвЛжжЩЬЦЗЕФНјМлЯрЭЌЃЌОпЬхЧщПіШчЯТБэЫљЪОЃК
СНжжЩЬЦЗНјааЯњЪлЃЌСНДЮЙКНјЭЌвЛжжЩЬЦЗЕФНјМлЯрЭЌЃЌОпЬхЧщПіШчЯТБэЫљЪОЃК
ЙКНјЪ§СПЃЈМўЃЉ | ЙКНјЫљашЗбгУЃЈдЊЃЉ | ||
|
| ||
ЕквЛДЮ | 30 | 40 | 3800 |
ЕкЖўДЮ | 40 | 30 | 3200 |
ЃЈ1ЃЉЧѓ![]() ЁЂ
ЁЂ![]() СНжжЩЬЦЗУПМўЕФНјМлЗжБ№ЪЧЖрЩйдЊЃП
СНжжЩЬЦЗУПМўЕФНјМлЗжБ№ЪЧЖрЩйдЊЃП
ЃЈ2ЃЉЩЬГЁОіЖЈ![]() жжЩЬЦЗвдУПМў30дЊГіЪлЃЌ
жжЩЬЦЗвдУПМў30дЊГіЪлЃЌ![]() жжЩЬЦЗвдУПМў100дЊГіЪлЃЎЮЊТњзуЪаГЁашЧѓЃЌашЙКНј
жжЩЬЦЗвдУПМў100дЊГіЪлЃЎЮЊТњзуЪаГЁашЧѓЃЌашЙКНј![]() ЁЂ
ЁЂ![]() СНжжЩЬЦЗЙВ1000МўЃЌЧв
СНжжЩЬЦЗЙВ1000МўЃЌЧв![]() жжЩЬЦЗЕФЪ§СПВЛЩйгк
жжЩЬЦЗЕФЪ§СПВЛЩйгк![]() жжЩЬЦЗЪ§СПЕФ4БЖЃЌЧыФуЧѓГіЛёРћзюДѓЕФНјЛѕЗНАИЃЌВЂШЗЖЈзюДѓРћШѓЃЎ
жжЩЬЦЗЪ§СПЕФ4БЖЃЌЧыФуЧѓГіЛёРћзюДѓЕФНјЛѕЗНАИЃЌВЂШЗЖЈзюДѓРћШѓЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
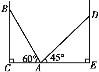
ЁОЬтФПЁПШчЭМЃЌдкСНУцЧНжЎМфгавЛИіЕзЖЫдкAЕуЕФЬнзгЃЌЕБЫќППдквЛВрЧНЩЯЪБЃЌЬнзгЕФЖЅЖЫдкBЕуЃЛЕБЫќППдкСэвЛВрЧНЩЯЪБЃЌЬнзгЕФЖЅЖЫдкDЕу.вбжЊЁЯBAC=60ЁуЃЌЁЯDAE=45ЁуЃЌЕуDЕНЕиУцЕФДЙжБОрРыDE=3 m.
(1)ЧѓСНУцЧНжЎМфОрРыCEЕФДѓаЁЃЛ
(2)ЧѓЕуBЕНЕиУцЕФДЙжБОрРыBCЕФДѓаЁ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
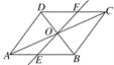
ЁОЬтФПЁПШчЭМЃЌдкЦНааЫФБпаЮABCDжаЃЌЖдНЧЯпACЃЌBDНЛгкЕуOЃЌОЙ§ЕуOЕФжБЯпНЛABгкEЃЌНЛCDгкFЃЌABЃН4ЃЌADЃН3ЃЌOFЃН1.3.ЧѓЫФБпаЮBCFEЕФжмГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЫцзХЁАЛЅСЊЭј+ЁБЪБДњЕФЕНРДЃЌвЛжжаТаЭДђГЕЗНЪНЪмЕНДѓжкЛЖгЃЌИУДђГЕЗНЪНЕФзмЗбгУгЩРяГЬЗбКЭКФЪБЗбзщГЩЃЌЦфжаРяГЬЗбАД![]() дЊ/ЙЋРяМЦЫуЃЌКФЪБЗбАД
дЊ/ЙЋРяМЦЫуЃЌКФЪБЗбАД![]() дЊ/ЗжжгМЦЫу(змЗбгУВЛзу
дЊ/ЗжжгМЦЫу(змЗбгУВЛзу![]() дЊАД
дЊАД![]() дЊМЦМл)ЃЎаЁУєЁЂаЁИеСНШЫгУИУДђГЕЗНЪНГіааЃЌАДЩЯЪіМЦМлЙцдђЃЌЦфааЪЛРяГЬЪ§ЁЂКФЪБвдМАДђГЕзмЗбгУШчЯТБэЃК
дЊМЦМл)ЃЎаЁУєЁЂаЁИеСНШЫгУИУДђГЕЗНЪНГіааЃЌАДЩЯЪіМЦМлЙцдђЃЌЦфааЪЛРяГЬЪ§ЁЂКФЪБвдМАДђГЕзмЗбгУШчЯТБэЃК
РяГЬЪ§ | КФЪБ | ГЕЗб(дЊ) | |
аЁУє |
|
|
|
аЁИе |
|
|
|
![]() Чѓ
Чѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
![]() ШєаЁЛЊвВгУИУДђГЕЗНЪНДђГЕЃЌЦНОљГЕЫйЮЊ
ШєаЁЛЊвВгУИУДђГЕЗНЪНДђГЕЃЌЦНОљГЕЫйЮЊ![]() ЙЋРя/ЪБЃЌааЪЛСЫ
ЙЋРя/ЪБЃЌааЪЛСЫ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНќФъРДЃЌЫцзХЮвЙњЕФПЦбЇММЪѕЕФбИУЭЗЂеЙЃЌКмЖраавЕвбОгЩЁАжаЙњжЦдьЁБЩ§МЖЮЊЁАжаЙњДДдьЁБЃЌИпЬњЪТвЕЪЧЁАжаЙњДДдьЁБЕФЕфЗЖЃЌвЛАуЕФИпЬњАќРЈGзжЭЗЕФИпЫйЖЏГЕзщвдМАDзжЭЗЕФЖЏГЕзщЃЎгЩДѓСЌЕНББОЉЕФG377ЕФЦНОљЫйЖШЪЧD31ЕФЦНОљЫйЖШЕФ1.2БЖЃЌааЪЛЯрЭЌЕФТЗГЬ1500ЧЇУзЃЌG377ЩйгУ1ИіаЁЪБЃЎ
ЃЈ1ЃЉЧѓD31ЕФЦНОљЫйЖШЃЎ
ЃЈ2ЃЉШєвдЁАЫйЖШгыЦБМлЕФБШжЕЁБЖЈвхетСНжжСаГЕЕФадМлБШЃЌШЫУЧГіааЖМЯВЛЖбЁдёадМлБШИпЕФЗНЪНЃЎЯжНзЖЮD31ЦБМлЮЊ266дЊ/еХЃЌG377ЦБМлЮЊ400дЊ/еХЃЌШчЙћФугаЛњЛсИјгаЙиВПУХЬсвЛИіКЯРэЛЏНЈвщЃЌЪЙG377ЕФадМлБШДяЕНD31ЕФадМлБШЃЌФуШчКЮНЈвщЃЌЮЊЪВУДЃП

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com