
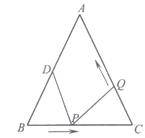
【题目】如图,已知在△ABC中,AB=AC=10cm,BC=8cm,D为AB中点,设点P在线段BC上以3cm/秒的速度由B点向C点运动,点Q在线段CA上由C点向A点运动.
(1)若Q点运动的速度与P点相同,且点P,Q同时出发,经过1秒钟后△BPD与△CQP是否全等,并说明理由;
(2)若点P,Q同时出发,但运动的速度不相同,当Q点的运动速度为多少时,能在运动过程中有△BPD与△CQP全等?
(3)若点Q以(2)中的速度从点C出发,点P以原来的速度从点B同时出发,都是逆时针沿△ABC的三边上运动,经过多少时间点P与点Q第一次在△ABC的哪条边上相遇?
【答案】(1)详见解析;(2)![]() cm/秒;(3)
cm/秒;(3)![]() 秒在AB边相遇.
秒在AB边相遇.
【解析】
(1)求出BD,CP,根据全等三角形的判定即可,
(2)由全等推出时间t,在利用CQ=BD求出Q的速度即可,
(3)求出Q的运动路程,根据△ABC的三边长度即可确定Q的位置.
(1)解:∵t=1秒,∴BP=CQ=3×1=3cm,
∵AB=10cm,点D为AB的中点,∴BD=5cm.
又∵PC=BC﹣BP,BC=8cm,∴PC=8﹣3=5cm,∴PC=BD.
又∵AB=AC,∴∠B=∠C,
在△BPD和△CQP中,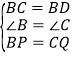
∴△BPD≌△CQP(SAS).
(2)解:∵vP≠vQ,
∴BP≠CQ,
又∵△BPD≌△CPQ,∠B=∠C,则BP=PC=4cm,CQ=BD=5cm,
∴点P,点Q运动的时间t=![]() 秒,∴vQ=
秒,∴vQ=![]() cm/秒;
cm/秒;
(3)设经过x秒后点P与点Q第一次相遇,
由题意,得 ![]() x=3x+2×10,解得x=
x=3x+2×10,解得x=![]() .
.
∴点P共运动了![]() ×3=80cm.∴80=56+24=2×28+24,∴点P、点Q在AB边上相遇,
×3=80cm.∴80=56+24=2×28+24,∴点P、点Q在AB边上相遇,
∴经过![]() 秒点P与点Q第一次在边AB上相遇.
秒点P与点Q第一次在边AB上相遇.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB⊥BC,AB∥DC,AB,BC,CD分别为2,2,2![]() +2,则∠BAD的度数等于( )
+2,则∠BAD的度数等于( )

A. 120° B. 135° C. 150° D. 以上都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,点E,F分别是边BC,AB上的点,且CE=BF,连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC.

(1)请判断:FG与CE的数量关系是__________,位置关系是__________;
(2)如图2,若点E、F分别是CB、BA延长线上的点,其它条件不变,(1)中结论是否仍然成立?请出判断判断并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将九年级部分男生掷实心球的成绩进行整理,分成5个小组(x表示成绩,单位:米).A组:5.25≤x<6.25;B组:6.25≤x<7.25;C组:7.25≤x<8.25;D组:8.25≤x<9.25;E组:9.25≤x<10.25,并绘制出扇形统计图和频数分布直方图(不完整).规定x≥6.25为合格,x≥9.25为优秀.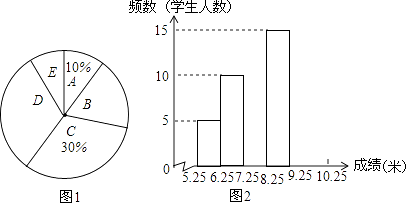
(1)这部分男生有多少人?其中成绩合格的有多少人?
(2)这部分男生成绩的中位数落在哪一组?扇形统计图中D组对应的圆心角是多少度?
(3)要从成绩优秀的学生中,随机选出2人介绍经验,已知甲、乙两位同学的成绩均为优秀,求他俩至少有1人被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示为一个污水净化塔内部,污水从上方入口进入后流经形如等腰直角三角形的净化材料表面,流向如图中箭头所示,每一次水流流经三角形两腰的机会相同,经过四层净化后流入底部的5个出口中的一个.下列判断:①5个出口的出水量相同;②2号出口的出水量与4号出口的出水量相同;③1,2,3号出水口的出水量之比约为1:4:6;④若净化材料损耗速度与流经其表面水的数量成正比,则更换最慢一个三角形材料使用的时间约为更换一个三角形材料使用时间的8倍,其中正确的判断有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次期中考试中,甲、乙、丙、丁、戊五位同学的数学、英语成绩等有关信息如下表所示(单位:分):
(1)求这五位同学在本次考试中数学成绩的平均分和英语成绩的标准差;
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,标准分的计算公式:标准分=(个人成绩-平均成绩)÷成绩标准差.
从标准分看,标准分大的考试成绩更好,请问甲同学在本次考试中,数学与英语哪个学科考得更好?
甲 | 乙 | 丙 | 丁 | 戊 | 平均分 | 标准差 | |
数学 | 71 | 72 | 69 | 68 | 70 | ||
英语 | 88 | 82 | 94 | 85 | 76 | 85 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】常用的分解因式的方法有提取公因式法、公式法,但有更多的多项式只用上述方法就无法分解,如x2﹣4y2﹣2x+4y,我们细心观察这个式子就会发现,前两项符合平方差公式,后两项可提取公因式,前后两部分分别分解因式后会产生公因式,然后提取公因式就可以完成整个式子的分解因式了,过程为:x2﹣4y2﹣2x+4y=(x+2y)(x﹣2y)﹣2(x﹣2y)=(x﹣2y)(x+2y﹣2),这种分解因式的方法叫分组分解法,利用这种方法解决下列问题.
(1)分解因式:x2+2xy+y2;
(2)分解因式:a2﹣9﹣2ab+b2;
(3)△ABC三边a、b、c满足a2﹣4bc+4ac﹣ab=0,判断△ABC的形状.
查看答案和解析>>
科目:初中数学 来源: 题型:
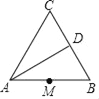
【题目】如图,在等边△ABC中,AB=4,角BAC的平分线交BC于点D,M为AB边中点,N是AD上的动点.
①在图上作出使得BN+MN的和最小时点N的位置,并说明理由.
②求出BN+MN的最小值.(提示:Rt△ABC中,∠C=90°,则有AC2+BC2=AB2成立)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com