

分析 (1)如图1中,作DH⊥BC于H,则四边形ABHD是矩形,AB=DH=8,AD=BH=4.当点N在BD上时,由MN∥DH,推出$\frac{MN}{DH}$=$\frac{BM}{BH}$,列出方程即可解决问题.当点N在CD上时,由tan∠C=$\frac{2}{3}$=$\frac{DH}{CH}$,得CH=12,由MN∥DH,得$\frac{MN}{DH}$=$\frac{CM}{CH}$,列出方程即可解决问题.
(2)分六种情形①如图2中,当0<t≤$\frac{3}{2}$时,重叠部分是△BKM.②如图3中,当$\frac{3}{2}$<t≤3时,重叠部分是四边形MNGB.③如图4中,当3<t≤$\frac{9}{2}$时,重叠部分是五边形MNGKF.④如图5中,当$\frac{9}{2}$<t≤$\frac{23}{2}$时,重叠部分是正方形MNEF,此时S=9.⑤如图6中,当$\frac{23}{2}$<t≤$\frac{29}{2}$时,重叠部分是五边形MKGEF.⑥如图7中,当$\frac{29}{2}$<t≤16时,重叠部分是四边形MKGF.分别求解即可.
(3)分三种情形①如图8中,当∠EQP=90°时.②如图9中,当∠QPE=90°.③如图10中,当∠QEP=90°,作EH⊥QP于H.设QH=x.由△QHE∽△EHP,得$\frac{QH}{EH}$=$\frac{EH}{PH}$,列出方程即可求解.
解答 解:(1)如图1中,作DH⊥BC于H,则四边形ABHD是矩形,AB=DH=8,AD=BH=4.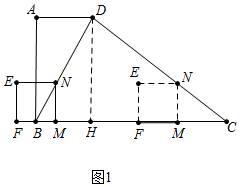
当点N在BD上时,∵MN∥DH,
∴$\frac{MN}{DH}$=$\frac{BM}{BH}$,
∴$\frac{3}{8}$=$\frac{t}{4}$,
∴t=$\frac{3}{2}$.
当点N在CD上时,∵tan∠C=$\frac{2}{3}$=$\frac{DH}{CH}$,
∴CH=12,
∵MN∥DH,
∴$\frac{MN}{DH}$=$\frac{CM}{CH}$,
∴$\frac{3}{8}$=$\frac{16-t}{12}$,
∴t=$\frac{23}{2}$.
∴t1=$\frac{3}{2}$,t2=$\frac{23}{2}$.
(2)①如图2中,当0<t≤$\frac{3}{2}$时,重叠部分是△BKM,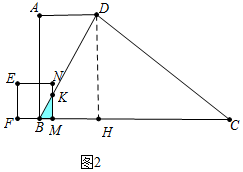
由$\frac{KM}{DH}$=$\frac{BM}{BH}$,得$\frac{KM}{8}$=$\frac{t}{4}$,
∴KM=2t,
∴S=$\frac{1}{2}$•t•2t=t2
②如图3中,当$\frac{3}{2}$<t≤3时,重叠部分是四边形MNGB,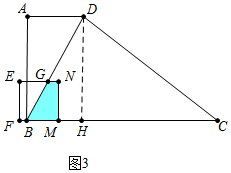
S=$\frac{1}{2}$•(t+t-$\frac{3}{2}$)•3=3t-$\frac{9}{4}$.
③如图4中,当3<t≤$\frac{9}{2}$时,重叠部分是五边形MNGKF.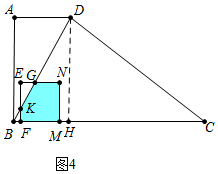
S=S正方形MNEF-S△EKG=9-$\frac{1}{2}$•(9-2t)•$\frac{1}{2}$(9-2t)=-t2+9t-$\frac{45}{4}$.
④如图5中,当$\frac{9}{2}$<t≤$\frac{23}{2}$时,重叠部分是正方形MNEF,此时S=9.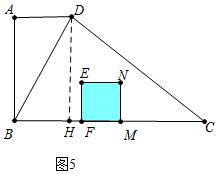
⑤如图6中,当$\frac{23}{2}$<t≤$\frac{29}{2}$时,重叠部分是五边形MKGEF,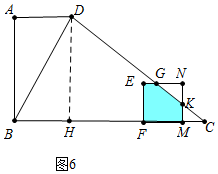
S=S正方形MNEF-S△NKG=9-$\frac{1}{2}$•[3-$\frac{2}{3}$(16-t)]•$\frac{3}{2}$[3-$\frac{2}{3}$(16-t)]=-$\frac{1}{3}$t2+$\frac{23}{3}$t-$\frac{529}{12}$.
⑥如图7中,当$\frac{29}{2}$<t≤16时,重叠部分是四边形MKGF.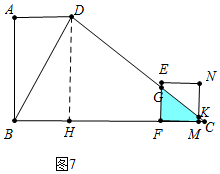
S=S△CFG-S△CKM=$\frac{1}{2}$•(19-t)•$\frac{2}{3}$(19-t)-$\frac{1}{2}$(16-t)•$\frac{2}{3}$(16-t)=35-2t.
综上所述,S=$\left\{\begin{array}{l}{{t}^{2}}&{(0<t≤\frac{3}{2})}\\{3t-\frac{9}{4}}&{(\frac{3}{2}<t≤3)}\\{-{t}^{2}+9t-\frac{45}{4}}&{(3<t≤\frac{9}{2})}\\{9}&{(\frac{9}{2}<t≤\frac{23}{2})}\\{-\frac{1}{3}{t}^{2}+\frac{23}{3}t-\frac{529}{12}}&{(\frac{23}{2}<t≤\frac{29}{2})}\\{35-2t}&{(\frac{29}{2}<t≤16)}\end{array}\right.$
(3)①如图8中,当∠EQP=90°时,由FQ=4,可知BF=2,∴t=2.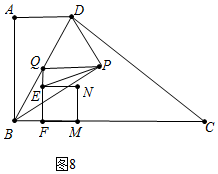
②如图9中,当∠QPE=90°,易知BF=2+2$\sqrt{5}$,∴t=2+2$\sqrt{5}$.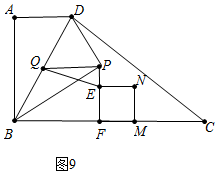
③如图10中,当∠QEP=90°,作EH⊥QP于H.设QH=x.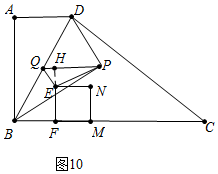
∵△QHE∽△EHP,
∴$\frac{QH}{EH}$=$\frac{EH}{PH}$,
∵HE=1,QH=x,PH=2$\sqrt{5}$-x,
∴x(2$\sqrt{5}$-x)=1,
∴x=$\sqrt{5}$±2,
∴BF=2+($\sqrt{5}$±2),
∴t=4+$\sqrt{5}$或$\sqrt{5}$.
综上所述,t=2s或(2+2$\sqrt{5}$)s或(4+$\sqrt{5}$)s或$\sqrt{5}$s时,△PQE是直角三角形.
点评 本题考查四边形综合题、正方形的性质、矩形的性质、平行线分线段成比例定理、相似三角形的判定和性质平移变换等知识,解题的关键是灵活运用所学知识解决问题,学会分类讨论,需要画好图形,利用图形解决问题,属于中考压轴题.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源: 题型:填空题
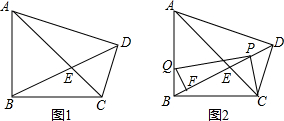
 如图,等腰△ABC中,AB=AC,BC∥x轴,点A、C在反比例函数y=$\frac{4}{x}$(x>0)的图象上,点B在反比例函数y=$\frac{1}{x}$(x>0)的图象上,则△ABC的面积为$\frac{9}{10}$.
如图,等腰△ABC中,AB=AC,BC∥x轴,点A、C在反比例函数y=$\frac{4}{x}$(x>0)的图象上,点B在反比例函数y=$\frac{1}{x}$(x>0)的图象上,则△ABC的面积为$\frac{9}{10}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,A、P、B、C是⊙O上的四个点,∠APC=∠CPB=60°.
如图,A、P、B、C是⊙O上的四个点,∠APC=∠CPB=60°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com