
【题目】已知:∠1=∠2,EG平分∠AEC.

(1)如图①,∠MAE=45°,∠FEG=15°,∠NCE=75°.求证:AB∥CD;
(2)如图②,∠MAE=140°,∠FEG=30°,当∠NCE= °时,AB∥CD;
(3)如图②,请你直接写出∠MAE、∠FEG、∠NCE之间满足什么关系时,AB∥CD;
(4)如图③,请你直接写出∠MAE、∠FEG、∠NCE之间满足什么关系时,AB∥CD.
【答案】(1)见解析;(2)当∠NCE=80°时,AB∥CD;(3)当2∠FEG+∠NCE=∠MAE时AB∥CD;(4)当∠MAE+2∠FEG+∠NCE=360°时,AB∥CD.
【解析】
(1)由题意可得AB∥EF,根据平行线的性质,角平分线的性质可得角的数量关系,可求∠FEC=75°,即可求结论.
(2)由题意可得AB∥EF,根据平行线的性质,角平分线的性质可得角的数量关系,可求∠FEC=100°,再根据AB∥CD,可求∠NCE的度数
(3)由题意可得AB∥EF,根据平行线的性质,角平分线的性质可得角的数量关系,可求∠FEC=180°-∠MAE+2∠FEG,再根据AB∥CD,可求其关系.
(4)由题意可得AB∥EF,根据平行线的性质,角平分线的性质可得角的数量关系,可求∠FEC=∠MAE+2∠FEG-180°,再根据AB∥CD,可求其关系.
证明(1)∵∠1=∠2
∴AB∥EF
∴∠MAE=∠AEF=45°,且∠FEG=15°
∴∠AEG=60°
∵EG平分∠AEC
∴∠AEG=∠CEG=60°
∴∠CEF=75°
∵∠ECN=75°
∴∠FEC=∠ECN
∴EF∥CD且AB∥EF
∴AB∥CD
(2)∵∠1=∠2
∴AB∥EF
∴∠MAE+∠FEA=180°且∠MAE=140°
∴∠AEF=40°
∵∠FEG=30°
∴∠AEG=70°
∵EG平分∠AEC
∴∠GEC=∠AEG=70°
∴∠FEC=100°
∵AB∥CD,AB∥EF
∴EF∥CD
∴∠NCE+∠FEC=180°
∴∠NCE=80°
∴当∠NCE=80°时,AB∥CD
(3)∵∠1=∠2
∴AB∥EF
∴∠MAE+∠FEA=180°
∴∠FEA=180°﹣∠MAE,
∴∠AEG=∠FEA+∠FEG=180°﹣∠MAE+∠FEG
∵EG平分∠AEC
∴∠GEC=∠AEG
∴∠FEC=∠GEC+∠FEG=180°﹣∠MAE+∠FEG+∠FEG=180°﹣∠MAE+2∠FEG
∵AB∥CD,AB∥EF
∴EF∥CD
∴∠FEC+∠NCE=180°
∴180°﹣∠MAE+2∠FEG+∠NCE=180°
∴2∠FEG+∠NCE=∠MAE
∴当2∠FEG+∠NCE=∠MAE时AB∥CD
(4)∠1=∠2
∴AB∥EF
∴∠MAE+∠FEA=180°
∴∠FEA=180°﹣∠MAE,
∴∠AEG=∠FEG﹣∠FEA=∠FEG﹣180°+∠MAE
∵EG平分∠AEC
∴∠GEC=∠AEG
∴∠FEC=∠FEA+2∠AEG=180°﹣∠MAE+2∠FEG﹣360°+2∠MAE=∠MAE+2∠FEG﹣180°
∵AB∥CD,AB∥EF
∴EF∥CD
∴∠FEC+∠NCE=180°
∴∠MAE+2∠FEG﹣180°+∠NCE=180°
∴∠MAE+2∠FEG+∠NCE=360°
∴当∠MAE+2∠FEG+∠NCE=360°时,AB∥CD


科目:初中数学 来源: 题型:
【题目】如图,C为线段AE上一动点(不与点A、E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°.
恒成立的结论有 .(把你认为正确的序号都填上)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰三角形,AB=AC,点D是AB上一点,过点D作DE⊥BC交BC于点E,交CA延长线于点F.
(1)证明:△ADF是等腰三角形;
(2)若∠B=60°,BD=4,AD=2,求EC的长,

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:在△ABC中,AB,BC,AC三边的长分别为![]() ,
,![]() ,
,![]() ,求此三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图①所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
,求此三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图①所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.

(1)请你将△ABC的面积直接填写在横线上:________.
思维拓展:
(2)我们把上述求△ABC面积的方法叫做构图法.如果△ABC三边的长分别为![]() a,
a,![]() a,
a,![]() a(a>0),请利用图②的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积.
a(a>0),请利用图②的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积.
探索创新:
(3)若△ABC三边的长分别为![]() ,
,![]() ,
,![]() (m>0,n>0,且m≠n),试运用构图法画出示意图并求出这三角形的面积.
(m>0,n>0,且m≠n),试运用构图法画出示意图并求出这三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解“阳光体育”活动的开展情况,从全校1000名学生中,随机抽取部分学生进行问卷调查(每名学生只能从A、B、C、D中选择一项自己喜欢的活动项目),并将调查结果绘制成如下两幅不完整的统计图.



A:踢毽子 B:乒乓球 C:篮球 D:跳绳
根据以上信息,解答下列问题:
(1)被调查的学生共有 人,并补全条形统计图;
(2)在扇形统计图中,求表示区域D的扇形圆心角的度数;
(3)全校学生中喜欢篮球的人数大约是多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B为定点,直线l∥AB,P是直线l上一动点.对于下列各值:①线段AB的长②△PAB的周长③△PAB的面积④∠APB的度数其中不会随点P的移动而变化的是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E在边CD上,将该矩形沿AE折叠,使点D落在边BC上的点F处,过点F作FG∥CD,交AE于点G,连接DG.

(1)求证:四边形DEFG为菱形;
(2)若CD=8,CF=4,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD平分∠BAC,∠C=90°,DE⊥AB于点E,点F在AC上,BD=DF.
(1)求证:CF=EB.
(2)若AB=12,AF=8,求CF的长。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD的顶点为A(1,2),B(﹣1,2),C(﹣1,﹣2),D(1,﹣2).点M和点N同时从E点出发,沿四边形的边做环绕匀速运动,M点以1单位/s的速度做逆时针运动,N点以2单位/s的速度做顺时针运动,则点M和点N第2016次相遇时的坐标为_____.
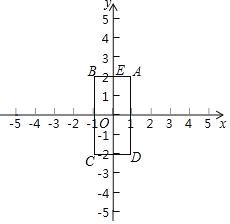
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com