
【题目】如图,在矩形ABCD中,点E在边CD上,将该矩形沿AE折叠,使点D落在边BC上的点F处,过点F作FG∥CD,交AE于点G,连接DG.

(1)求证:四边形DEFG为菱形;
(2)若CD=8,CF=4,求![]() 的值.
的值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】(1)如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.求证:CE=CF;
(2)如图2,在正方形ABCD中,E是AB上一点,G是AD上一点,如果∠GCE=45°,请你利用(1)的结论证明:GE=BE+GD.
(3)运用(1)(2)解答中所积累的经验和知识,完成下题:
如图3,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC,E是AB上一点,且∠DCE=45°,BE=4,DE="10," 求直角梯形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CD是AB边上的中线,E是CD的中点,过点C作AB的平行线交AE的延长线于点F,连接BF.
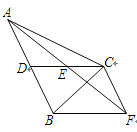
(1) 求证:CF=AD;
(2) 若CA=CB,∠ACB=90°,试判断四边形CDBF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AE⊥BC于点E,延长BC至点F使CF=BE,连结AF,DE,DF.
(1)求证:四边形AEFD是矩形;
(2)若AB=6,DE=8,BF=10,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=4,则四边形OCED的周长为( )
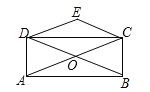
A.4B.8C.10D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】弹簧挂上适当的重物后会按一定的规律伸长,已知一弹簧的长度![]() (cm)与所挂物体的质量
(cm)与所挂物体的质量![]() (kg)之间的关系如下表:
(kg)之间的关系如下表:
所挂物体的质量 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
弹簧的长度 | 15 | 15.6 | 16.2 | 16.8 | 17.4 | 18 | 18.6 |
(1)上表反映了哪两个变量之间的关系?哪个是自变量?
(2)写出![]() 与
与![]() 之间的关系式;
之间的关系式;
(3)当物体的质量逐渐增加时,弹簧的长度怎样变化?
(4)当所挂物体的质量为11.5kg时,求弹簧的长度。
查看答案和解析>>
科目:初中数学 来源: 题型:
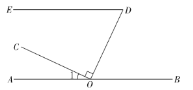
【题目】如图,点O在直线AB上,OC⊥OD,∠EDO与∠1互余.
(1)求证:ED//AB;
(2)OF平分∠COD交DE于点F,若∠OFD=65°,补全图形,并求∠1的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com