
【题目】在平行四边形![]() 中,
中, ![]() ,
, ![]() ,过点
,过点![]() 作
作![]() 垂直直线
垂直直线![]() 于点
于点![]() ,
, ![]() ,再过点
,再过点![]() 作
作![]() 垂直于直线
垂直于直线![]() 于点
于点![]() ,则
,则![]() __________.
__________.
【答案】4.5或13.5
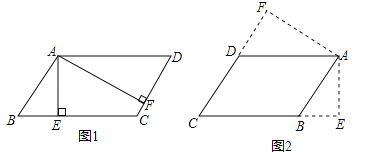
【解析】解:如图,∵BC=5,AE⊥BC,AE=![]() ,∴平行四边形ABCD的面积为:BCAE=5×
,∴平行四边形ABCD的面积为:BCAE=5×![]() =
=![]() .∵四边形ABCD是平行四边形,∴AB=CD=4,BC=AD=5.
.∵四边形ABCD是平行四边形,∴AB=CD=4,BC=AD=5.
①由平行四边形面积公式得:BC×AE=CD×AF=![]() ,则AF=
,则AF=![]() .
.
在Rt△ABE和Rt△ADF中,由勾股定理得:AB2=AE2+BE2,把AB=4,AE=![]() 代入求出BE=2,同理DF=
代入求出BE=2,同理DF=![]() <4,即F在线段DC上(如图1),∴CE=5﹣2=3,CF=4﹣
<4,即F在线段DC上(如图1),∴CE=5﹣2=3,CF=4﹣![]() =
=![]() ,即CE+CF=3+
,即CE+CF=3+![]() =4.5;
=4.5;
②如图:∵AB=4,AE=![]() ,在△ABE中,由勾股定理得:BE=
,在△ABE中,由勾股定理得:BE=![]() =
=![]() =2,同理DF=
=2,同理DF=![]() .
.
则CE=BC+BE=5+2=7,CF=CD+DF=4+![]() =6.5,∴CE+CF=7+6.5=13.5;
=6.5,∴CE+CF=7+6.5=13.5;
故答案为:4.5或13.5.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,⊙![]() 半径为
半径为![]() ,
, ![]() 是⊙
是⊙![]() 的直径,点
的直径,点![]() 为
为![]() 延长线上一点,动点
延长线上一点,动点![]() 从点
从点![]() 出发以
出发以![]() 的速度沿
的速度沿![]() 方向运动,同时,动点
方向运动,同时,动点![]() 从点
从点![]() 出发以
出发以![]() 的速度沿
的速度沿![]() 方向运动,当两点相遇时都停止运动.过点
方向运动,当两点相遇时都停止运动.过点![]() 作
作![]() 的垂线,与⊙
的垂线,与⊙![]() 分别交于点
分别交于点![]() 、
、![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]() .
.
(![]() )当四边形
)当四边形![]() 是正方形时,
是正方形时, ![]() __________
__________ ![]() ,
, ![]() __________
__________ ![]() .
.
(![]() )当四边形
)当四边形![]() 是菱形且
是菱形且![]() 时,求
时,求![]() 内切圆的半径.
内切圆的半径.
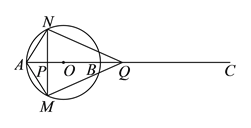
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中每个小方格的边长为1,且点A,B,C均为格点.

(1)画出△ABC关于直线l的对称图形△A1B1C1;
(2)求△ABC的面积;
(3)边AB=_____________(不用写过程);
(4)在直线l上找一点D,使AD+BD最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD的两条对角线相交于点O,过点 A作AG⊥BD分别交BD、BC于点G、E.

(1)求证:BE2=EGEA;
(2)连接CG,若BE=CE,求证:∠ECG=∠EAC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E在边CD上,将该矩形沿AE折叠,使点D落在边BC上的点F处,过点F作FG∥CD,交AE于点G,连接DG.

(1)求证:四边形DEFG为菱形;
(2)若CD=8,CF=4,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为加强学生安全意识,组织全校学生参加安全知识竞赛。从中抽取部分学生成绩(得分取正整数值,满分为100分)进行统计,绘制以下两幅不完整的统计图.

请根据图中的信息,解决下列问题:
(1)填空:a=_____,n=_____;
(2)补全频数直方图;
(3)该校共有2000名学生.若成绩在70分以下(含70分)的学生安全意识不强,则该校安全意识不强的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.

(1)在给定方格纸中画出平移后的△A′B′C′;
(2)画出AB边上的中线CD和BC边上的高线AE;
(3) 求四边形ACBB′的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将自然数按以下规律排列:

表中数2在第二行第一列,与有序数对(2,1)对应,数5与(1,3)对应,数14与(3,4)对应,根据这一规律,数2014对应的有序数对为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究:在边长为![]() 的正方形
的正方形![]() 中,对角线
中,对角线![]() 、
、![]() 交于点
交于点![]() .
.
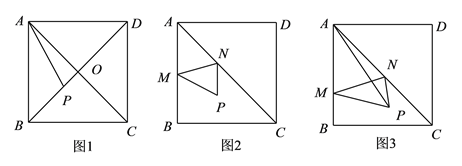
探究![]() :如图
:如图![]() ,若点
,若点![]() 是对角线
是对角线![]() 上任意一点,则线段
上任意一点,则线段![]() 的长的取值范围是__________;
的长的取值范围是__________;
探究![]() :如图
:如图![]() ,若点
,若点![]() 是
是![]() 内任意一点,点
内任意一点,点![]() 、
、![]() 分别是
分别是![]() 边和对角线
边和对角线![]() 上的两个动点,则当
上的两个动点,则当![]() 的值在探究
的值在探究![]() 中的取值范围内变化时,
中的取值范围内变化时, ![]() 的周长是否存在最小值?如果存在,请求出
的周长是否存在最小值?如果存在,请求出![]() 周长的最小值,若不存在,请说明理由;
周长的最小值,若不存在,请说明理由;
问题解决:如图![]() ,在边长为
,在边长为![]() 的正方形
的正方形![]() 中,点
中,点![]() 是
是![]() 内任意一点,且
内任意一点,且![]() ,点
,点![]() 、
、![]() 分别是
分别是![]() 边和对角线
边和对角线![]() 上的两个动点,则当
上的两个动点,则当![]() 的周长取到最小值时,求四边形
的周长取到最小值时,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com