
【题目】如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=4,则四边形OCED的周长为( )
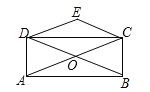
A.4B.8C.10D.12
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:
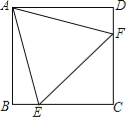
【题目】如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④S正方形ABCD=![]() .
.
其中正确的序号是 (把你认为正确的都填上).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】本商场为了吸引顾客,设立了一个可以自由转动的转盘,如图所示,并规定,顾客消费100元以上(不包括100元),就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准打折区域顾客就可以获得此项待遇(转盘等分成8份,指针停在每个区域的机会相等).
(1)顾客小华消费150元,获得打折待遇的概率是多少?
(2)顾客小明消费120元,获得五折待遇的概率是多少?
(3)小华对小明说:“我们用这个转盘来做一个游戏,指针指到五折你赢,指针指到七折算我赢”,你认为这个游戏规则公平吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,正方形A1B1C1D1、D1 E1E2B2、A2B2 C2D2、D2 E3E4B3……按如图所示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3……在x轴上,已知正方形A1B1C1D1的边长为l,∠B1C1O= 60°, B1C1∥B2C2∥B3C3……,则正方形A2017B2017 C2017 D2017的边长是( )

A. (![]() )2016 B. (
)2016 B. (![]() )2017 C. (
)2017 C. (![]() )2016 D. (
)2016 D. (![]() )2017
)2017
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,DB∥AC,且DB=![]() AC,E是AC的中点,
AC,E是AC的中点,
(1)求证:BC=DE;
(2)连接AD、BE,若要使四边形DBEA是矩形,则给△ABC添加什么条件,为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E在边CD上,将该矩形沿AE折叠,使点D落在边BC上的点F处,过点F作FG∥CD,交AE于点G,连接DG.

(1)求证:四边形DEFG为菱形;
(2)若CD=8,CF=4,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:设一元二次方程![]() (
(![]() ≠0)的两根为
≠0)的两根为![]() ,
, ![]() ,则两根与方程的系数之间有如下关系:
,则两根与方程的系数之间有如下关系:
![]() +
+![]() =-
=-![]() ,
, ![]() ·
·![]() =
=![]() .根据该材料完成下列填空:
.根据该材料完成下列填空:
已知![]() ,
, ![]() 是方程
是方程![]() 的两根,则(1)
的两根,则(1)![]() +
+ ![]() =_________,
=_________, ![]() __________;(2)(
__________;(2)(![]() )(
)(![]() )=__________.
)=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①若式子![]() 有意义,则
有意义,则![]() 的取值范围是
的取值范围是![]() ;②正多边形的的一个内角是140°,则这个多边形是正九边形;③甲、乙两人进行射击测试,每人次射击成绩的平均数都是8.8环,方差分别是
;②正多边形的的一个内角是140°,则这个多边形是正九边形;③甲、乙两人进行射击测试,每人次射击成绩的平均数都是8.8环,方差分别是![]() ,
,![]() ,则射击成绩最稳定的是乙;④若
,则射击成绩最稳定的是乙;④若![]() 是方程
是方程![]() 的一个实数根,则
的一个实数根,则![]() 的值是4.其中正确的有( )个
的值是4.其中正确的有( )个
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某化妆品专卖店,为了吸引顾客,准备在“母亲节”当天举办了甲、乙两种品牌化妆品有奖酬宾活动,凡购物满![]() 元,均可得到一次摇奖的机会.已知在摇奖机内装有
元,均可得到一次摇奖的机会.已知在摇奖机内装有![]() 个红球和
个红球和![]() 个白球,除颜色外其它都相同,摇奖者必须从摇奖机中一次连续摇出两个球,根据球的颜色决定送礼金券的多少(如下表):
个白球,除颜色外其它都相同,摇奖者必须从摇奖机中一次连续摇出两个球,根据球的颜色决定送礼金券的多少(如下表):

(![]() )请你用列表法(或画树状图法)求一次连续摇出一红一白两球的概率;
)请你用列表法(或画树状图法)求一次连续摇出一红一白两球的概率;
(![]() )如果一个顾客当天在本店购物满
)如果一个顾客当天在本店购物满![]() 元,若只考虑获得最多的礼品卷,请你帮助分析选择购买哪种品牌的化妆品?并说明理由.
元,若只考虑获得最多的礼品卷,请你帮助分析选择购买哪种品牌的化妆品?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com