
【题目】某化妆品专卖店,为了吸引顾客,准备在“母亲节”当天举办了甲、乙两种品牌化妆品有奖酬宾活动,凡购物满![]() 元,均可得到一次摇奖的机会.已知在摇奖机内装有
元,均可得到一次摇奖的机会.已知在摇奖机内装有![]() 个红球和
个红球和![]() 个白球,除颜色外其它都相同,摇奖者必须从摇奖机中一次连续摇出两个球,根据球的颜色决定送礼金券的多少(如下表):
个白球,除颜色外其它都相同,摇奖者必须从摇奖机中一次连续摇出两个球,根据球的颜色决定送礼金券的多少(如下表):

(![]() )请你用列表法(或画树状图法)求一次连续摇出一红一白两球的概率;
)请你用列表法(或画树状图法)求一次连续摇出一红一白两球的概率;
(![]() )如果一个顾客当天在本店购物满
)如果一个顾客当天在本店购物满![]() 元,若只考虑获得最多的礼品卷,请你帮助分析选择购买哪种品牌的化妆品?并说明理由.
元,若只考虑获得最多的礼品卷,请你帮助分析选择购买哪种品牌的化妆品?并说明理由.
【答案】(![]() )树状图见解析,
)树状图见解析, ![]() ;(
;(![]() )甲,理由见解析.
)甲,理由见解析.
【解析】试题分析:(1)摇奖机内有两红两白球,标记为红1,红2,白1,白2,连续摇出一红一白,先出来的球有四种情况,且概率相等,分别为红1,红2,白1,白2,画出树状图,再写出后出来球的情况,如上图所示进而找出一红一白的结果有8种,占所有可能出现的结果12种的三分之二.
(2)先在(1)的基础上再算出另外两种情况出现的概率,根据算出的概率,依据甲乙化妆品获得礼品券的方案分别算出获得礼品券,取获得礼品券多的品牌化妆品.
试题解析:(1)用树状图列出所有可能的结果:
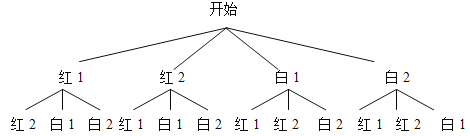
由树状图可知,所有可能出现的结果共有12种,且每种结果出现的可能性相同,其中恰好连续摇出一红一白的结果有8种,所以P(一红一白)=![]() .∴一次连续摇出一红一白两球的概率为
.∴一次连续摇出一红一白两球的概率为![]() .
.
(2)若顾客在本店购物满88元,由(1)得:P(两红)=![]() , P(两白)=
, P(两白)=![]() .
.
(3)若购买甲品牌化妆品,则获得礼品卷为6×![]() +12×
+12×![]() +6×
+6×![]() =10(元);若购买乙品牌化妆品,则获得礼品卷为12×
=10(元);若购买乙品牌化妆品,则获得礼品卷为12×![]() +6×
+6×![]() +12×
+12×![]() =8(元).∵10>8,∴顾客应选择购买甲品牌的化妆品.
=8(元).∵10>8,∴顾客应选择购买甲品牌的化妆品.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=4,则四边形OCED的周长为( )
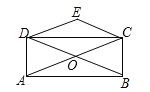
A.4B.8C.10D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】ABCD中,E是CD边上一点,
(1)将△ADE绕点A按顺时针方向旋转,使AD、AB重合,得到△ABF,如图1所示.观察可知:与DE相等的线段是 ,∠AFB=∠
(2)如图2,正方形ABCD中,P、Q分别是BC、CD边上的点,且∠PAQ=45°,试通过旋转的方式说明:DQ+BP=PQ;
(3)在(2)题中,连接BD分别交AP、AQ于M、N,你还能用旋转的思想说明BM2+DN2=MN2吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】AC是□ABCD的一条对角线,过AC中点O的直线分别交AD、BC 于点E、F.

(1)求证:AE=CF;
(2)连接AF,CE.
①当EF⊥AC时,四边形AFCE是什么四边形?请证明你的结论;
②若AB=1,BC=2,∠B=60°,则四边形AFCE为矩形时,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点B,C分别是∠MAN的边AM、AN上的点,满足AB=BC,点P为射线的AB上的动点,点D为点B关于直线AC的对称点,连接PD交AC于E点,交BC于点F。
(1)在图1中补全图形;
(2)求证:∠ABE=∠EFC;
(3)当点P运动到满足PD⊥BE的位置时,在射线AC上取点Q,使得AE=EQ,此时![]() 是否是一个定值,若是请直接写出该定值,若不是,请说明理由.
是否是一个定值,若是请直接写出该定值,若不是,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
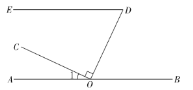
【题目】如图,点O在直线AB上,OC⊥OD,∠EDO与∠1互余.
(1)求证:ED//AB;
(2)OF平分∠COD交DE于点F,若∠OFD=65°,补全图形,并求∠1的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C是⊙O上一点,过点C的直线交AB的延长线于点D,AE⊥DC,垂足为E,F是AE与⊙O的交点,AC平分∠BAE,连接OC.
(1)求证:DE是⊙O的切线;
(2)若⊙O半径为4,∠D=30°,求图中阴影部分的面积(结果用含π和根号的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读以下材料,并按要求完成相应的任务.
在初中数学课本中重点介绍了提公因式法和运用公式法两种因式
分解的方法,其中运用公式法即运用平方差公式:![]() 和完全平方公式:
和完全平方公式:![]() 进行分解因式,能运用完全平方公式分解因式的多项式必须是三项式,其中有两项能写成两个数(或式)的平方和的形式,另一项是这两个数(或式)的积的2倍.当一个二次三项式不能直接能运用完全平方公式分解因式时,可应用下面方法分解因式,先将多项式
进行分解因式,能运用完全平方公式分解因式的多项式必须是三项式,其中有两项能写成两个数(或式)的平方和的形式,另一项是这两个数(或式)的积的2倍.当一个二次三项式不能直接能运用完全平方公式分解因式时,可应用下面方法分解因式,先将多项式![]()
![]() 变形为
变形为![]() 的形式,我们把这样的变形方法叫做多项式
的形式,我们把这样的变形方法叫做多项式![]() 的配方法.再运用多项式的配方法及平方差公式能对一些多项式进行分解因式.
的配方法.再运用多项式的配方法及平方差公式能对一些多项式进行分解因式.
例如:![]()
![]()

![]()
![]() .
.
根据以上材料,完成相应的任务:
(1)利用“多项式的配方法”将![]() 化成
化成![]() 的形式为_______;
的形式为_______;
(2)请你利用上述方法因式分解:
①![]() ; ②
; ②![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com