
【题目】ABCD中,E是CD边上一点,
(1)将△ADE绕点A按顺时针方向旋转,使AD、AB重合,得到△ABF,如图1所示.观察可知:与DE相等的线段是 ,∠AFB=∠
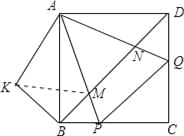
(2)如图2,正方形ABCD中,P、Q分别是BC、CD边上的点,且∠PAQ=45°,试通过旋转的方式说明:DQ+BP=PQ;
(3)在(2)题中,连接BD分别交AP、AQ于M、N,你还能用旋转的思想说明BM2+DN2=MN2吗?

【答案】(1)BF,AED;(2)证明见解析;(3)证明见解析.
【解析】试题分析:(1)、直接根据旋转的性质得到DE=BF,∠AFB=∠AED;(2)、将△ADQ绕点A按顺时针方向旋转90°,则AD与AB重合,得到△ABE,根据旋转的性质得∠EAQ=∠BAD=90°,AE=AQ,BE=DQ,而∠PAQ=45°,则∠PAE=45°,再根据全等三角形的判定方法得到△APE≌△APQ,则PE=PQ,于是PE=PB+BE=PB+DQ,即可得到DQ+BP=PQ;
(3)、根据正方形的性质有∠ABD=∠ADB=45°,将△ADN绕点A按顺时针方向旋转90°,则AD与AB重合,得到△ABK,根据旋转的性质得∠ABK=∠ADN=45°,BK=DN,AK=AN,与(2)一样可证明△AMN≌△AMK得到MN=MK,由于∠MBA+∠KBA=45°+45°=90°,得到△BMK为直角三角形,根据勾股定理得BK2+BM2=MK2,然后利用等相等代换即可得到BM2+DN2=MN2.
试题解析:(1)、∵△ADE绕点A按顺时针方向旋转,使AD、AB重合,得到△ABF,
∵DE=BF,∠AFB=∠AED.
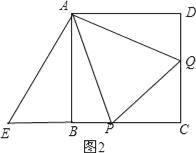
(2)、将△ADQ绕点A按顺时针方向旋转90°,则AD与AB重合,得到△ABE,如图2,
则∠D=∠ABE=90°, 即点E、B、P共线,∠EAQ=∠BAD=90°,AE=AQ,BE=DQ, ∵∠PAQ=45°,
∴∠PAE=45° ∴∠PAQ=∠PAE, ∴△APE≌△APQ(SAS), ∴PE=PQ,
而PE=PB+BE=PB+DQ, ∴DQ+BP=PQ;
(3)、∵四边形ABCD为正方形, ∴∠ABD=∠ADB=45°,
如图,将△ADN绕点A按顺时针方向旋转90°,则AD与AB重合,得到△ABK,
则∠ABK=∠ADN=45°,BK=DN,AK=AN, 与(2)一样可证明△AMN≌△AMK,得到MN=MK,
∵∠MBA+∠KBA=45°+45°=90°, ∴△BMK为直角三角形, ∴BK2+BM2=MK2, ∴BM2+DN2=MN2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】辽宁号航空母舰是中国人民解放军海军第一艘服役的航空母舰.满载时排水量为67500吨,将数据67500用科学记数法表示为( )
A.6.75×103B.6.75×104C.0.675×105D.675×102
查看答案和解析>>
科目:初中数学 来源: 题型:
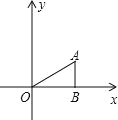
【题目】如图,△ABO中,AB⊥OB,OB=![]() ,AB=1,把△ABO绕点O旋转150°后得到△A1B1O,则点A1的坐标为( )
,AB=1,把△ABO绕点O旋转150°后得到△A1B1O,则点A1的坐标为( )
A.(﹣1,-![]() )
)
B.(﹣1,-![]() )或(﹣2,0)
)或(﹣2,0)
C.(-![]() ,﹣1)或(0,﹣2)
,﹣1)或(0,﹣2)
D.(-![]() ,﹣1)
,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果A和B都是5次多项式,则下面说法正确的是( )
A.A﹣B一定是多项式
B.A﹣B是次数不低于5的整式
C.A+B一定是单项式
D.A+B是次数不高于5的整式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四个小长方形,图②是边长为m-n的正方形.
(1)请用图①中四个小长方形和图②中的正方形拼成一个大正方形,画出示意图(要求连接处既没有重叠,也没有空隙);
(2)请用两种不同的方法列代数式表示(1)中拼得的大正方形的面积;
(3)请直接写出(m+n)2,(m-n)2,mn这三个代数式之间的等量关系;
(4)根据(4)中的等量关系,解决如下问题:若a+b=6,ab=4,求(a-b)2的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OE⊥AB,OF⊥CD, 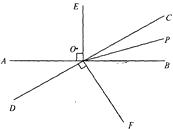
(1)图中除直角外,还有相等的角吗?请写出两对:①;② .
(2)如果∠AOD=40°,则①∠BOC=;②OP是∠BOC的平分线,所以∠COP=度;③求∠BOF的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com