
【题目】如图,在△ABC中,CD是AB边上的中线,E是CD的中点,过点C作AB的平行线交AE的延长线于点F,连接BF.
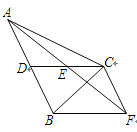
(1) 求证:CF=AD;
(2) 若CA=CB,∠ACB=90°,试判断四边形CDBF的形状,并说明理由.
【答案】见解析;正方形.
【解析】
试题(1)、根据CF∥AB可得∠CFE=∠DAE,∠FCE=∠ADE,根据E为中点可得CE=DE,则△ECF和△DEA全等,从而得出答案;(2)、根据AD=BD,则CF=BD,CF∥BD得出平行四边形,根据CD为AB边上的中线,CA=CB得出∠BDC=90°得出矩形,根据CD为等腰直角△ABC斜边上的中线得出CD=BD,即得到正方形.
试题解析:(1)、∵CF∥AB,∴∠CFE=∠DAE,∠FCE=∠ADE,∵E为CD的中点,∴CE=DE,
∴△ECF≌△DEA(AAS), ∴CF=AD,
(2)四边形CDBF为正方形,理由为:
∵AD=BD, ∴CF=BD; ∵CF=BD,CF∥BD,∴四边形CDBF为平行四边形,
∵CA=CB,CD为AB边上的中线,∴CD⊥AB,即∠BDC=90°,∴四边形CDBF为矩形,
∵等腰直角△ABC中,CD为斜边上的中线,∴CD=![]() AB,即CD=BD,则四边形CDBF为正方形.
AB,即CD=BD,则四边形CDBF为正方形.


 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
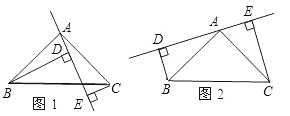
【题目】如图1,△ABC中,AB=AC,∠BAC=90°,直线l经过点A,过B、C两点分别作直线l的垂线段,垂足分别为D、E.
(1)如图1,△ABD与与△CAE全等吗?请说明理由;
(2)如图1,BD=DE+CE成立吗?为什么?
(3)若直线AE绕A点旋转到如图2位置时,其它条件不变,BD与DE、CE关系如何?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为深化义务教育课程改革,满足学生的个性化学习需求,某校就“学生对知识拓展、体育特长、艺术特长和时间活动四类选课意向”进行了抽样调查(每人选报一类),绘制了如图所示的两幅统计图(不完整),请根据图中信息,解答下列问题.
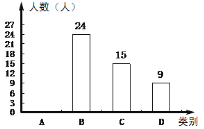
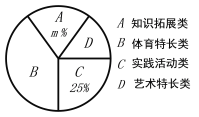
(1)求扇形统计图中的m的值,并补全条形统计图;
(2)已知该校800名学生,计划开设“实践活动类”课程,每班安排20人,问学校开设多少个“实践活动课”课程的班级比较合理.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若(a+b)2=21,大正方形的面积为13,则小正方形的面积为
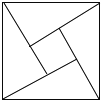
A. 3B. 4C. 5D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】本商场为了吸引顾客,设立了一个可以自由转动的转盘,如图所示,并规定,顾客消费100元以上(不包括100元),就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准打折区域顾客就可以获得此项待遇(转盘等分成8份,指针停在每个区域的机会相等).
(1)顾客小华消费150元,获得打折待遇的概率是多少?
(2)顾客小明消费120元,获得五折待遇的概率是多少?
(3)小华对小明说:“我们用这个转盘来做一个游戏,指针指到五折你赢,指针指到七折算我赢”,你认为这个游戏规则公平吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中每个小方格的边长为1,且点A,B,C均为格点.

(1)画出△ABC关于直线l的对称图形△A1B1C1;
(2)求△ABC的面积;
(3)边AB=_____________(不用写过程);
(4)在直线l上找一点D,使AD+BD最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,正方形A1B1C1D1、D1 E1E2B2、A2B2 C2D2、D2 E3E4B3……按如图所示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3……在x轴上,已知正方形A1B1C1D1的边长为l,∠B1C1O= 60°, B1C1∥B2C2∥B3C3……,则正方形A2017B2017 C2017 D2017的边长是( )

A. (![]() )2016 B. (
)2016 B. (![]() )2017 C. (
)2017 C. (![]() )2016 D. (
)2016 D. (![]() )2017
)2017
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E在边CD上,将该矩形沿AE折叠,使点D落在边BC上的点F处,过点F作FG∥CD,交AE于点G,连接DG.

(1)求证:四边形DEFG为菱形;
(2)若CD=8,CF=4,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图四边形![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .动点
.动点![]() 从点
从点![]() 出发,沿射线
出发,沿射线![]() 的方向以每秒
的方向以每秒![]() 的速度运动到
的速度运动到![]() 点返回,动点
点返回,动点![]() 从点
从点![]() 出发,在线段
出发,在线段![]() 上以每秒
上以每秒![]() 的速度向点
的速度向点![]() 运动,点
运动,点![]() ,
,![]() 分别从点
分别从点![]() ,
,![]() 同时出发,当点
同时出发,当点![]() 运动到点
运动到点![]() 时,点
时,点![]() 停止运动,设运动时间为
停止运动,设运动时间为![]() (秒).
(秒).
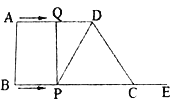

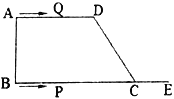

(1)当![]() 时,是否存在点
时,是否存在点![]() ,使四边形
,使四边形![]() 是平行四边形,若存在,求出
是平行四边形,若存在,求出![]() 值;若不存在,请说明理由;
值;若不存在,请说明理由;
(2)当![]() 为何值时,以
为何值时,以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形面积等于
为顶点的四边形面积等于![]() ;
;
(3)当![]() 时,是否存在点
时,是否存在点![]() ,使
,使![]() 是等腰三角形?若存在,请直接写出所有满足要求的
是等腰三角形?若存在,请直接写出所有满足要求的![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com