
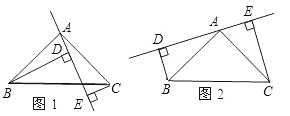
【题目】如图1,△ABC中,AB=AC,∠BAC=90°,直线l经过点A,过B、C两点分别作直线l的垂线段,垂足分别为D、E.
(1)如图1,△ABD与与△CAE全等吗?请说明理由;
(2)如图1,BD=DE+CE成立吗?为什么?
(3)若直线AE绕A点旋转到如图2位置时,其它条件不变,BD与DE、CE关系如何?请说明理由.
【答案】(1)△ABD≌△CAE;(2)成立;(3)DE=BD+CE.
【解析】
(1)根据已知条件易证得∠BAD=∠ACE,且根据全等三角形的判定可证明△ABD≌△CAE;
(2)根据全等三角形的性质及各线段的关系即可得结论.
(3)DE=BD+CE.根据全等三角形的判定可证明△ABD≌△CAE,根据各线段的关系即可得结论.
(1)△ABD≌△CAE,理由如下:
∵∠BAC=90°,∴∠BAD+∠CAE=90°.
∵CE⊥AE,∴∠ACE+∠CAE=90°,∴∠ACE=∠BAD;
又∵BD⊥AE,CE⊥AE,∴∠ADB=∠CEA=90°.
在△ABD和△CAE中,∵∠BAD=∠ACE,∠ADB=∠CEA,AB=CA,∴△ABD≌△CAE(AAS);
(2)成立,理由如下:
∵△ABD≌△CAE,∴BD=AE,AD=CE;
∵AE=DE+AD,∴BD=DE+CE;
(3)DE=BD+CE.理由如下:
∵∠BAC=90°,∴∠BAD+∠CAE=90°.
∵CE⊥AE,∴∠ACE+∠CAE=90°,∴∠ACE=∠BAD;
又∵BD⊥AE,CE⊥AE,∴∠ADB=∠CEA=90°.
在△ABD和△CAE中,∵∠BAD=∠ACE,∠ADB=∠CEA,AB=CA,∴△ABD≌△CAE(AAS),∴BD=AE,AD=CE;
∵DE=AE+AD,∴DE=BD+CE.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:
【题目】某商厦进货员预测一种应季衬衫能畅销市场,就用![]() 万元购进这种衬衫,面市后果然供不应求.商厦又用
万元购进这种衬衫,面市后果然供不应求.商厦又用![]() 万元购进第二批这种衬衫,所购数量是第一批进量的
万元购进第二批这种衬衫,所购数量是第一批进量的![]() 倍,但单价贵了
倍,但单价贵了![]() 元.商厦销售这种衬衫时每件定价
元.商厦销售这种衬衫时每件定价![]() 元,最后剩下
元,最后剩下![]() 件按八折销售,很快售完.在这两笔生意中,商厦共盈利多少元?
件按八折销售,很快售完.在这两笔生意中,商厦共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“如图1,在Rt△ABC中,∠ACB=90°,CD是△ABC的高,则△ACD与△CBD相似吗?”于是,学生甲发现CD2=AD·BD也成立.
问题1:请你证明CD2=AD·BD;

学生乙从CD2=AD·BD中得出:可以画出两条已知线段的比例中项.
问题2:已知两条线段AB、BC在x轴上,如图2:请你用直尺(无刻度)和圆规作出这两条线段的比例中项.要求保留作图痕迹,不要写作法,最后指出所要作的线段.

学生丙也从CD2=AD·BD中悟出了矩形与正方形的等积作法.
问题3:如图3,已知矩形ABCD,请你用直尺(无刻度)和圆规作出一个正方形BMNP,使得S正方形BMNP=S矩形ABCD.要求:保留作图痕迹;简要写出作图每个步骤的要点.

查看答案和解析>>
科目:初中数学 来源: 题型:
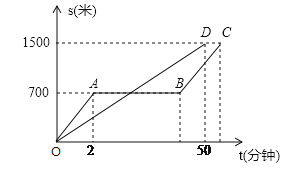
【题目】“龟免赛跑”的故事同学们都非常热悉,图中的线段OD和折线OABC表示“龟兔赛跑时路程与时间的关系,请你根据图中给出的信息,解决下列问题.
(1)填空:折线OABC表示赛跑过程中_______(填“兔子”或“乌龟”)的路程与时间的关系,赛跑的全过程是___________米.
(2)兔子在起初每分钟跑多少米?乌龟每分钟爬多少米?
(3)乌龟用了多少分钟追上了正在睡觉的兔子?
(4)兔子醒来假,以400米/分的速度跑向终点,结果还是比乌龟晚到了0.5分钟,请你算算兔子中间停下睡觉用了多少分钟.
查看答案和解析>>
科目:初中数学 来源: 题型:
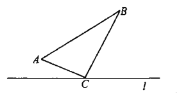
【题目】如图,![]() 中,
中,![]() .点
.点![]() 从点
从点![]() 出发沿
出发沿![]() 路径向终点
路径向终点![]() 运动;点
运动;点![]() 从
从![]() 点出发沿
点出发沿![]() 路径向终点
路径向终点![]() 运动.点
运动.点![]() 和
和![]() 分别以1和3的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过
分别以1和3的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过![]() 和
和![]() 作
作![]() 于
于![]() ,
,![]() 于
于![]() .则点
.则点![]() 运动时间等于____________时,
运动时间等于____________时,![]() 与
与![]() 全等。
全等。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.求证:CE=CF;
(2)如图2,在正方形ABCD中,E是AB上一点,G是AD上一点,如果∠GCE=45°,请你利用(1)的结论证明:GE=BE+GD.
(3)运用(1)(2)解答中所积累的经验和知识,完成下题:
如图3,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC,E是AB上一点,且∠DCE=45°,BE=4,DE="10," 求直角梯形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CD是AB边上的中线,E是CD的中点,过点C作AB的平行线交AE的延长线于点F,连接BF.
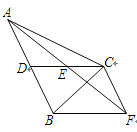
(1) 求证:CF=AD;
(2) 若CA=CB,∠ACB=90°,试判断四边形CDBF的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com