
【题目】“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若(a+b)2=21,大正方形的面积为13,则小正方形的面积为
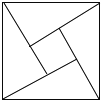
A. 3B. 4C. 5D. 8
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
【题目】“如图1,在Rt△ABC中,∠ACB=90°,CD是△ABC的高,则△ACD与△CBD相似吗?”于是,学生甲发现CD2=AD·BD也成立.
问题1:请你证明CD2=AD·BD;

学生乙从CD2=AD·BD中得出:可以画出两条已知线段的比例中项.
问题2:已知两条线段AB、BC在x轴上,如图2:请你用直尺(无刻度)和圆规作出这两条线段的比例中项.要求保留作图痕迹,不要写作法,最后指出所要作的线段.

学生丙也从CD2=AD·BD中悟出了矩形与正方形的等积作法.
问题3:如图3,已知矩形ABCD,请你用直尺(无刻度)和圆规作出一个正方形BMNP,使得S正方形BMNP=S矩形ABCD.要求:保留作图痕迹;简要写出作图每个步骤的要点.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.求证:CE=CF;
(2)如图2,在正方形ABCD中,E是AB上一点,G是AD上一点,如果∠GCE=45°,请你利用(1)的结论证明:GE=BE+GD.
(3)运用(1)(2)解答中所积累的经验和知识,完成下题:
如图3,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC,E是AB上一点,且∠DCE=45°,BE=4,DE="10," 求直角梯形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,⊙P经过x轴上一点C,与y轴分别相交于A、B两点,连接AP并延长分别交⊙P、x轴于点D、点E,连接DC并延长交y轴于点F.若点F的坐标为![]() ,点D的坐标为
,点D的坐标为![]() .
.
(1)求证:DC=FC;
(2)判断⊙P与x轴的位置关系,并说明理由;
(3)求⊙P的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线AB与CD相交于点O,OE、OF分别是∠BOD、∠AOD的平分线。
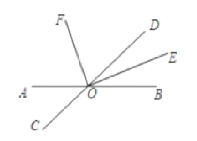
(1)∠DOE的补角是___;
(2)若∠BOD=62°,求∠AOE和∠DOF的度数;
(3)判断射线OE与OF之间有怎样的位置关系?并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程(k-1)x2+2kx+2=0
(1)求证:无论k为何值,方程总有实数根.
(2)设x1,x2是该方程的两个根,记S=x1+x2-x1x2,S的值能为0吗?若能,求出此时k的值.若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CD是AB边上的中线,E是CD的中点,过点C作AB的平行线交AE的延长线于点F,连接BF.
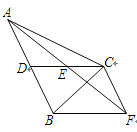
(1) 求证:CF=AD;
(2) 若CA=CB,∠ACB=90°,试判断四边形CDBF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AE⊥BC于点E,延长BC至点F使CF=BE,连结AF,DE,DF.
(1)求证:四边形AEFD是矩形;
(2)若AB=6,DE=8,BF=10,求AE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com