
【题目】如图,在平面直角坐标系中,⊙P经过x轴上一点C,与y轴分别相交于A、B两点,连接AP并延长分别交⊙P、x轴于点D、点E,连接DC并延长交y轴于点F.若点F的坐标为![]() ,点D的坐标为
,点D的坐标为![]() .
.
(1)求证:DC=FC;
(2)判断⊙P与x轴的位置关系,并说明理由;
(3)求⊙P的半径.

【答案】(1)证明见解析;(2)⊙P与x轴相切.理由见解析;(3)5.
【解析】(1)证明:过点D作DH⊥x轴于点H,则∠CHD=∠COF =90°.
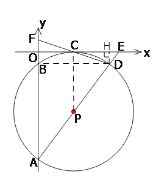 ∵点F的坐标为(0,1),点D的坐标为(6,-1),∴DH=OF,
∵点F的坐标为(0,1),点D的坐标为(6,-1),∴DH=OF,
∵在△FOC与△DHC中,
![]() ∠FCO=∠DCH
∠FCO=∠DCH
∠FOC=∠DHC=90°
OF=HD
∴△FOC≌△DHC(AAS),
∴DC=FC;
(2)答:⊙P与x轴相切.理由如下:
如图,连接CP.
∵AP=PD,DC=CF,
∴CP∥AF,
∴∠PCE=∠AOC=90°,即PC⊥x轴.
又PC是半径,
∴⊙P与x轴相切;
(3)解:由(2)可知,CP是△DFA的中位线,
∴AF=2CP.∵AD=2CP,
∴AD=AF.连接BD.
∵AD是⊙P的直径,
∴∠ABD=90°,
∴BD=OH=6,OB=DH=FO=1.
设AD的长为x,则在直角△ABD中,由勾股定理,得
x2=62+(x-2)2,解得 x=10.
∴⊙![]() 的半径为5.
的半径为5.


科目:初中数学 来源: 题型:
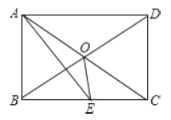
【题目】如图所示,矩形ABCD中,AE平分![]() 交BC于E,
交BC于E,![]() ,则下面的结论:①
,则下面的结论:①![]() 是等边三角形;②
是等边三角形;②![]() ;③
;③![]() ;④
;④![]() ,其中正确结论有( )
,其中正确结论有( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() 为坐标原点.已知:抛物线
为坐标原点.已知:抛物线![]() 经过点
经过点![]() 和点
和点![]() .
.
(![]() )试判断该抛物线与
)试判断该抛物线与![]() 轴交点的情况.
轴交点的情况.
(![]() )平移这条抛物线,使平移后的抛物线经过点
)平移这条抛物线,使平移后的抛物线经过点![]() ,且与
,且与![]() 轴交于点
轴交于点![]() ,同时满足以
,同时满足以![]() ,
, ![]() ,
, ![]() 为顶点的三角形是等腰直角三角形.请你写出平移过程,并说明理由.
为顶点的三角形是等腰直角三角形.请你写出平移过程,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙![]() 半径为
半径为![]() ,
, ![]() 是⊙
是⊙![]() 的直径,点
的直径,点![]() 为
为![]() 延长线上一点,动点
延长线上一点,动点![]() 从点
从点![]() 出发以
出发以![]() 的速度沿
的速度沿![]() 方向运动,同时,动点
方向运动,同时,动点![]() 从点
从点![]() 出发以
出发以![]() 的速度沿
的速度沿![]() 方向运动,当两点相遇时都停止运动.过点
方向运动,当两点相遇时都停止运动.过点![]() 作
作![]() 的垂线,与⊙
的垂线,与⊙![]() 分别交于点
分别交于点![]() 、
、![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]() .
.
(![]() )当四边形
)当四边形![]() 是正方形时,
是正方形时, ![]() __________
__________ ![]() ,
, ![]() __________
__________ ![]() .
.
(![]() )当四边形
)当四边形![]() 是菱形且
是菱形且![]() 时,求
时,求![]() 内切圆的半径.
内切圆的半径.
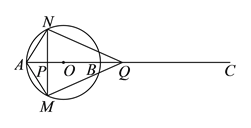
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为深化义务教育课程改革,满足学生的个性化学习需求,某校就“学生对知识拓展、体育特长、艺术特长和时间活动四类选课意向”进行了抽样调查(每人选报一类),绘制了如图所示的两幅统计图(不完整),请根据图中信息,解答下列问题.
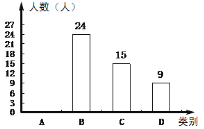
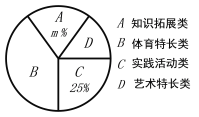
(1)求扇形统计图中的m的值,并补全条形统计图;
(2)已知该校800名学生,计划开设“实践活动类”课程,每班安排20人,问学校开设多少个“实践活动课”课程的班级比较合理.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形![]() 分别是边
分别是边![]() 上的点,
上的点,![]() 分别是
分别是![]() 的中点,当点
的中点,当点![]() 在
在![]() 上从点
上从点![]() 向点
向点![]() 移动而点
移动而点![]() 不动时,线段
不动时,线段![]() 的长__________ (填“会”或“不会”) 发生变化,如果不发生改变求出
的长__________ (填“会”或“不会”) 发生变化,如果不发生改变求出![]() 的长(直接将答案填写横线上);如果
的长(直接将答案填写横线上);如果![]() 的长会改变说明理由.请把你认为的结论写出来
的长会改变说明理由.请把你认为的结论写出来

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若(a+b)2=21,大正方形的面积为13,则小正方形的面积为
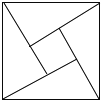
A. 3B. 4C. 5D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中每个小方格的边长为1,且点A,B,C均为格点.

(1)画出△ABC关于直线l的对称图形△A1B1C1;
(2)求△ABC的面积;
(3)边AB=_____________(不用写过程);
(4)在直线l上找一点D,使AD+BD最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.

(1)在给定方格纸中画出平移后的△A′B′C′;
(2)画出AB边上的中线CD和BC边上的高线AE;
(3) 求四边形ACBB′的面积
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com