
【题目】如图,已知矩形![]() 分别是边
分别是边![]() 上的点,
上的点,![]() 分别是
分别是![]() 的中点,当点
的中点,当点![]() 在
在![]() 上从点
上从点![]() 向点
向点![]() 移动而点
移动而点![]() 不动时,线段
不动时,线段![]() 的长__________ (填“会”或“不会”) 发生变化,如果不发生改变求出
的长__________ (填“会”或“不会”) 发生变化,如果不发生改变求出![]() 的长(直接将答案填写横线上);如果
的长(直接将答案填写横线上);如果![]() 的长会改变说明理由.请把你认为的结论写出来
的长会改变说明理由.请把你认为的结论写出来

【答案】不会;理由见解析,PQ的长为![]() cm.
cm.
【解析】
连接AF,根据P,Q分别是AE,EF的中点,可得PQ是三角形AEF的中位线,即PQ=![]() AF,AF的长不变,即可得PQ的长不会发生变化.
AF,AF的长不变,即可得PQ的长不会发生变化.
解:线段PQ的长不会发生变化,理由如下:
如图,连接AF,

∵P,Q分别是AE,EF的中点,
∴PQ是三角形AEF的中位线,
∴PQ=![]() AF,
AF,
∵四边形ABCD是矩形,
∴∠B=90°,AB=CD=4cm,
在Rt△ABF中,BF=9cm,AB=40cm,
根据勾股定理,得AF=![]() (cm),
(cm),
因为AF的长不变,
所以PQ的长不会发生变化,
∴PQ=![]() AF=
AF=![]() (cm).
(cm).
故答案为:不会;结论为:线段PQ的长不会发生变化,PQ的长为![]() cm.
cm.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
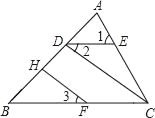
【题目】已知,如图,∠1=∠ACB,∠2=∠3,FH⊥AB于H,求证:CD⊥AB.请将下面的推理过程补充完整.
证明:FH⊥AB(已知)
∴∠BHF= °.( )
∵∠1=∠ACB(已知)
∴DE∥BC( )
∴∠2= .( )
∵∠2=∠3(已知)
∴∠3= .( )
∴CD∥FH( )
∴∠BDC=∠BHF= °.( )
∴CD⊥AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E是BC的中点,连接AE并延长交DC的延长线于点F.

(1)求证:AB=CF;
(2)连接DE,若AD=2AB,求证:DE⊥AF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,⊙P经过x轴上一点C,与y轴分别相交于A、B两点,连接AP并延长分别交⊙P、x轴于点D、点E,连接DC并延长交y轴于点F.若点F的坐标为![]() ,点D的坐标为
,点D的坐标为![]() .
.
(1)求证:DC=FC;
(2)判断⊙P与x轴的位置关系,并说明理由;
(3)求⊙P的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D、E分别在钱段AB、AC上,CD与BE交于O,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD

A. ∠B=∠CB. AD=AEC. BE=CDD. BD=CE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程(k-1)x2+2kx+2=0
(1)求证:无论k为何值,方程总有实数根.
(2)设x1,x2是该方程的两个根,记S=x1+x2-x1x2,S的值能为0吗?若能,求出此时k的值.若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在菱形ABCD 中,点E,O,F分别是边AB,AC,AD的中点,连接CE、CF、OE、OF.当AB与BC满足___________条件时,四边形AEOF正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“你今天光盘了吗?”这是国家倡导厉行节约,反对浪费以来的时尚流行语,某校团委随机抽取部分了学生,对他们是否了解关于“光盘行动”的情况进行调查,调查结果有三种:A、了解很多;B、了解一点;C、不了解.团委根据调查的数据进行整理,绘制了尚不完整的统计图如下,图1中C区域的圆心角为36°,请根据统计图中的相关的信息,解答下列问题:

(1)求本次活动共调查了多少名学生?
(2)请补全图2,并求出图1中,B区域的圆心角度数;
(3)若该校有2400名学生,请估算该校不是了解很多的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com