
 ��ͼ��ֱ��y=-3x+3��x�ᡢy��ֱ��ڵ�A��B��������y=a��x-2��2+k����A��B������x�ύ����һ��C���䶥��ΪP��
��ͼ��ֱ��y=-3x+3��x�ᡢy��ֱ��ڵ�A��B��������y=a��x-2��2+k����A��B������x�ύ����һ��C���䶥��ΪP������ ��1���������������A��B���꣬���������߽���ʽ�����a��k��ֵ��
��2����B��ƽ��x���ֱ�ߣ���B������ֱ��ȡ�߶�BQ1=BQ2=AC����C��ƽ��AB��ֱ�ߣ���C������ֱ��ȡCQ3=CQ4=AB����Q3��Q4��x��ľ��붼����B�㵽x��ľ��룬�ɷֱ��������������Q������ꣻ
��3����A��C���ڶԳ���Գƣ�����BC���Գ����ڵ�M����M��Ϊ������B��C�����ֱ��BC�Ľ���ʽ�������M������꣬����������ܳ���
��4������N������Ϊ��2��n�����ɷֱ��ʾ��AB��AN��BN�ij����ɹ��ɶ����ɵõ�����n����̣������N�����꣮
��� �⣺��1����y=-3x+3�У���y=0�������x=1����x=0�������y=3��
��A��1��0����B��0��3����
�ֱ����y=a��x-2��2+k���ɵ�$\left\{\begin{array}{l}{a+k=0}\\{4a+k=3}\end{array}\right.$�����$\left\{\begin{array}{l}{a=1}\\{k=-1}\end{array}\right.$��
��aΪ1��kΪ-1��
��2���ɣ�1����֪�����߽���ʽΪy=��x-2��2-1��
��y=0�������x=1��x=3��
��C��3��0����
��AC=3-1=2��AB=$\sqrt{10}$��
��B��ƽ��x���ֱ�ߣ���B������ֱ��ȡ�߶�BQ1=BQ2=AC=2����ͼ1��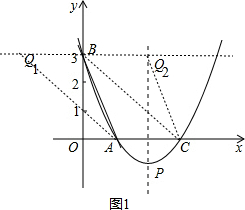
��B��0��3����
��Q1��-2��3����Q2��2��3����
��C��AB��ƽ���ߣ���C��ֱ������ȡCQ3=CQ4=AB=$\sqrt{10}$����ͼ2��
��B��0��3����
��Q3��Q4��x��ľ��붼����B�㵽x��ľ���ҲΪ3���ҵ�ֱ��x=3�ľ���Ϊ1��
��Q3��2��3����Q4��4��-3����
���Ͽ�֪����������Q�������Ϊ��-2��3����2��3����4��-3����
��3����������֪�Գ��᷽��Ϊx=2������BC���Գ����ڵ�M������MA����ͼ3��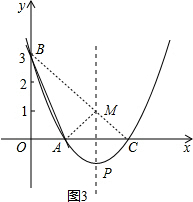
��A��C������ڶԳ���Գƣ�
��AM=MC��
��BM+AM����
���ABM�ܳ���С��
��B��0��3����C��3��0����
�����ֱ��BC����ʽΪy=mx+3��
��C�������������m=-1��
��ֱ��BC����ʽΪy=-x+3��
��x=2ʱ���ɵ�y=1��
��M��2��1����
���������������M�㣬
��ʱBC=3$\sqrt{2}$����AB=$\sqrt{10}$��
���ABM���ܳ�����СֵΪ3$\sqrt{2}$+$\sqrt{10}$��
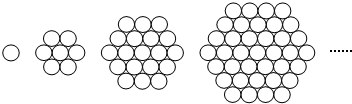
��4������������N��������2��n����
��NB2=22+��n-3��2=n2-6n+13��NA2=��2-1��2+n2=1+n2����AB2=10��
����ABNΪ��ABΪб�ߵ�ֱ��������ʱ���ɹ��ɶ����ɵ�NB2+NA2=AB2��
��n2-6n+13+1+n2=10�����n=1��n=2��
��N��������2��1����2��2����
���Ͽ�֪��������������N�㣬������Ϊ��2��1����2��2����
���� ������Ҫ������κ�����Ӧ�ã��漰����ϵ������ƽ���ı��ε����ʡ���ԳƵ����ʡ����ɶ�����֪ʶ�㣮�ڣ�1�������A��B����������ǽ���Ĺؼ����ڣ�2����ȷ����Q���λ���ǽ���Ĺؼ����ڣ�3����ȷ����M���λ���ǽ���Ĺؼ����ڣ�4�������N�����꣬���ù��ɶ����õ������ǽ���Ĺؼ��������漰֪ʶ��϶࣬�ۺ��Խ�ǿ���Ѷ����У�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �Խ����ഹֱƽ�� | B�� | �ڽǺ�Ϊ360�� | ||
| C�� | �Խ������ | D�� | �Խ���ƽ���ڽ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 91 | B�� | 109 | C�� | 127 | D�� | 18 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com