
| A�� | ����װ��һ������������������dz���ɫ�ⶼ��ͬ���������������һ��������ɫ��Żأ����ҡ�����ٴ������������һ��������������ͬ��ɫ��ĸ�����$\frac{4}{9}$ | |
| B�� | �ס��������桰ʯͷ����������������Ϸ����Ϸ�����ǣ�������˵�������ͬ����ô�����˱���ʤ������������Ʋ�ͬ�����ա�ʯͷʤ����������ʤ������ʤʯͷ���Ĺ�������ס��ҵĻ�ʤ�ߣ������Ϸ������ڼס��ҡ��������ǹ�ƽ�� | |
| C�� | ��������ö�ʵؾ��ȵ�Ӳ�ң�����ö���泯�ϡ�������ö���泯�ϡ��͡�һö���泯�ϣ�һö���泯�ϡ��������ֽ�������ĸ�������ͬ�� | |
| D�� | һ��С��İ���ͬѧͨ�����γ�ǩ����Ƭ���һ�����鵽���Żأ�����һ��ͬѧ���Ԫ����Ʒ���ȳ�ͺ���ͬѧ��ý�Ʒ�ĸ�������ͬ�ģ���ǩ���Ⱥ�Ӱ�칫ƽ |
���� ���ݸ��ʵ��������Ϸ�Ĺ�ƽ�Խ����жϼ��ɣ�
��� �⣺A������װ��һ������������������dz���ɫ�ⶼ��ͬ���������������һ��������ɫ��Żأ����ҡ�����ٴ������������һ��������������ͬ��ɫ��ĸ�����$\frac{4}{9}$����ȷ��
B���ס��������桰ʯͷ����������������Ϸ����Ϸ�����ǣ�������˵�������ͬ����ô�����˱���ʤ������������Ʋ�ͬ�����ա�ʯͷʤ����������ʤ������ʤʯͷ���Ĺ�������ס��ҵĻ�ʤ�ߣ������Ϸ������ڼס��ҡ��������ǹ�ƽ�ģ���ȷ��
C����������ö�ʵؾ��ȵ�Ӳ�ң�����ö���泯�ϡ�������ö���泯�ϡ��͡�һö���泯�ϣ�һö���泯�ϡ��������ֽ�������ĸ����Dz�ͬ�ģ�����
D��С��İ���ͬѧͨ�����γ�ǩ����Ƭ���һ�����鵽���Żأ�����һ��ͬѧ���Ԫ����Ʒ���ȳ�ͺ���ͬѧ��ý�Ʒ�ĸ�������ͬ�ģ���ǩ���Ⱥ�Ӱ�칫ƽ����ȷ��
��ѡC
���� ���⿼���˸��ʵ����壬������Ϸ�Ĺ�ƽ�ԣ����ݸ���=������������������֮�Ƚ���ǹؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
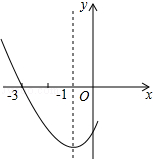 ��ͼ���������ϵ�������y=ax2+bx+c�ĶԳ���Ϊֱ��x=-1���ҹ��㣨-3��0��������˵������abc��0����b-2a=0����4a+2b+c��0��������$\frac{5}{2}$��y1������-5��y2���������������㣬��y1��y2��������ȷ�ĸ����ǣ�������
��ͼ���������ϵ�������y=ax2+bx+c�ĶԳ���Ϊֱ��x=-1���ҹ��㣨-3��0��������˵������abc��0����b-2a=0����4a+2b+c��0��������$\frac{5}{2}$��y1������-5��y2���������������㣬��y1��y2��������ȷ�ĸ����ǣ�������| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ƽ��ֱ������ϵ�У���O������ԭ�㣬A��0��6����B��$2\sqrt{3}$��0�����ҡ�OBA=60�㣬����OAB��ֱ��AB���ۣ��õ���CAB����O���C��Ӧ��
��ͼ����ƽ��ֱ������ϵ�У���O������ԭ�㣬A��0��6����B��$2\sqrt{3}$��0�����ҡ�OBA=60�㣬����OAB��ֱ��AB���ۣ��õ���CAB����O���C��Ӧ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3�� | B�� | 4�� | C�� | 5�� | D�� | 6�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 1 | C�� | -1 | D�� | ������ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �ǵı�Խ������Խ�� | |
| B�� | ����֮����߶Σ��������ľ��� | |
| C�� | ��A��B��P��ͬһֱ���ϣ���AB=2AP����P��AB���е� | |
| D�� | �ڡ�AOB����һ������OC������AOC=��BOC��������OCƽ�֡�AOB |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | -2 | C�� | 0 | D�� | -1.5 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com