【题目】如图，直线y=ax+b与抛物线y=ax2+bx+c的图象在同一坐标系中可能是（ ）
A.
B.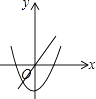
C.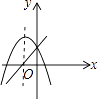
D.
【答案】B
【解析】解：①当a＞0时，二次函数的图象应该开口向上，一次函数的图象应该在一三或一二三或一三四象限，不正确；②一次函数的图象反映的信息是：a＞0，b=0，此时二次函数的图象应该开口向上，且对称轴为x=0，正确；③一次函数的图象反映的信息是：a＞0，b＞0，此时二次函数的图象应该开口向下，a＜0，不正确；④一次函数的图象反映的信息是：a＞0，b＜0，此时二次函数的图象应该开口向下，a＜0，不正确；故选B．
【考点精析】本题主要考查了一次函数的图象和性质和二次函数的图象的相关知识点，需要掌握一次函数是直线，图像经过仨象限；正比例函数更简单,经过原点一直线；两个系数k与b,作用之大莫小看，k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减；k为负来左下展,变化规律正相反；k的绝对值越大,线离横轴就越远；二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点才能正确解答此题．
应用题作业本系列答案
暑假作业暑假快乐练西安出版社系列答案科目：初中数学 来源： 题型：
【题目】已知直线l与直线l外一点P，求作：过点P且垂直于直线l的垂线a（尺规作图）．
现给出一种作法，如下：
步骤一：在直线l外取一点E，以点P为圆心，以线段PE为半径画弧，交直线l于点M，N；
步骤二：分别以点M、N为圆心，大于
线段MN为半径画弧，过两弧的交点的直线a就是所求作的垂线．
（1）按上述操作步骤，请成功作出过点P且垂直于直线l的垂线a．（符合要求的一种图形），并说明理由．
（2）从你作图的过程中，思考要保证这种作法顺利作出，线段PE应该满足什么条件？
（3）为了避免这种情况产生，小明说只要在直线l上取点E好了，并给出了画法，画法对吗？请说明理由．
（作法：在直线l上取两点B、D，以P为圆心，以PD 为半径画圆交直线l于点E，以P为圆心，以PB 为半径画圆交直线l于点F，其中较小圆分别交PB，PF于点M、N，连接E、N和D、M，EN和MD相交于点H，则PH就是所求的垂线．）
（4）请在直线l上取点E，用直尺和圆规过点P且垂直于直线l的垂线a（与小明不同的方法，并要求尽可能简单）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示,直线AB,CD,EF相交于点O,∠DOB的度数是它余角的2,∠AOE=2∠DOF,OG⊥AB.
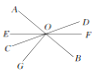
求：(1)∠DOB的度数;
(2)∠BOF的度数;
(3)∠EOG的度数.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】用配方法解一元二次方程x2-6x-1=0时，方程可变形为（ ）
A. （x-3）2=10 B. （x-6）2=37 C. （x-3）2=4 D. （x-3）2=1
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知抛物线 y= 
x2﹣2x的顶点是A，与x轴相交于点B、C两点（点B在点C的左侧）．
（1）求A、B、C的坐标；
（2）直接写出当y＜0时x的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，某工厂与A、B两地有公路、铁路相连．这家工厂从A地购买一批每吨2000元的原料运回工厂，制成每吨7500元的产品运到B地．已知公路运价为2元/ (吨·千米)，铁路运价为 1.5元/(吨·千米)，且这两次运输共支出公路运输费2.6万元，铁路运输费15.6万元。
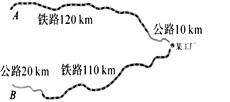
求：(1)该工厂从A地购买了多少吨原料？ 制成运往B地的产品多少吨？
(2)若不计人力成本，这批产品盈利多少元？ （盈利=销售款-原料费-运输费）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com