练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
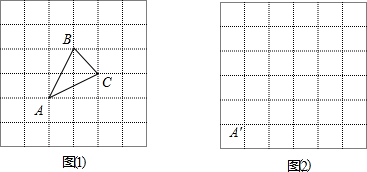
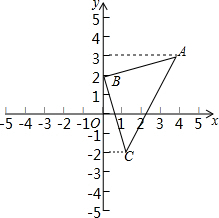    3．如图，利用关于坐标轴对称的点的坐标的特点，作出△ABC关于x轴对称的图形．

    分析 根据轴对称的性质画出图形即可．

    解答 解：如图所示：

    点评 本题考查的是作图-轴对称变换，熟知关于x轴对称的点的坐标特点是解答此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

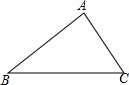    13．如图，三角形ABC中，∠BAC=70°，点D是射线BC上一点（不与点B、C重合），DE∥AB交直线AC于E，DF∥AC交直线AB于F，则∠FDE的度数为70°或110°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

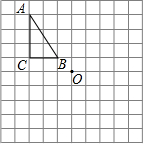    14．已知，如图△ABC，请在网格纸中画．
    （1）下移5，左移1个单位；
    （2）△ABC关于O点成中心对称图形；
    （3）△ABC以点O为旋转中心，顺时针旋转90°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．△ABC中，AD是BC边上中线，E为AD上一点，BE的延长线交AC于F，交AB的平行线CG于G．证明：BE2=EF•EG．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．数学课上，李老师出示了这样一道题目：如图1，正方形ABCD的边长为12，P为边BC延长线上的一点，E为DP的中点，DP的垂直平分线交边DC于M，交边AB的延长线于N．当CP=6时，EM与EN的比值是多少？
    经过思考，小明展示了一种正确的解题思路：过E作直线平行于BC交DC，AB分别于F，G，如图2，则可得：$\frac{DF}{FC}=\frac{DE}{EP}$，因为DE=EP，所以DF=FC．可求出EF和EG的值，进而可求得EM与EN的比值．
    （1）请按照小明的思路写出求解过程．
    （2）小东又对此题作了进一步探究，得出了DP=MN的结论．你认为小东的这个结论正确吗？如果正确，请给予证明；如果不正确，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．我国现行个人工资薪金税征收办法规定：月收入低于800元但低于1300元的部分征收5%的所得税…如某人某月收入1160元，他应缴个人工资薪金所得税为（1160-800）×5%=18（元）
    ①当月收入大于800元而又小于1300元时，写出应缴所得税y（元）与月收入x（元）之间的关系式y=0.05x-40；
    ②某人某月收入为960元，他应缴所得税8元；
    ③如果某人本月缴所得税19.2元，那么此人本月工资薪金是1184元．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

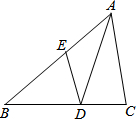    15．如图，在△ABC中，AD是角平分线，点E在AB上，且DE∥CA．
    （1）△BDE与△BCA相似吗？为什么？
    （2）已知AB=8，AC=6，求DE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．阅读下列材料：
    正方形网格中，每个小正方形的顶点称为格点，以格点为顶点的三角形叫格点三角形．数学老师给小明同学出了一道题目：在图（1）正方形网格（每个小正方形边长为1）中画出格点△ABC，使AB=AC=$\sqrt{5}$，BC=$\sqrt{2}$；小明同学的做法是：由勾股定理，得AB=AC=$\sqrt{{2^2}+{1^2}}=\sqrt{5}$，BC=$\sqrt{{1^2}+{1^2}}=\sqrt{2}$，于是画出线段AB、AC、BC，从而画出格点△ABC．
    （1）请你参考小明同学的做法，在图（2）正方形网格（每个小正方形边长为1）中画出格点△A′B′C′（A′点位置如图所示），使A′B′=A′C′=5，B′C′=$\sqrt{10}$．（直接画出图形，不写过程）；
    （2）观察△ABC与△A′B′C′的形状，猜想∠BAC与∠B′A′C′有怎样的数量关系，并证明你的猜想．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

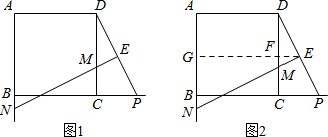
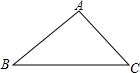    13．某厂有一块如图所示的△ABC铜板，根据需要，现要把它加工成一个平行四边形铜板，要把材料完全利用起来，可怎样加工？请你利用学过的知识帮助工人师傅把切割的线用虚线画出来，并指出加工后的平行四边形，能否将此三角形铜板加工成长方形？请给出说明．

    查看答案和解析>>

    同步练习册答案