
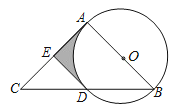
【题目】如图,AB是⊙O的直径,AC是⊙O的切线,切点为A,BC交⊙O于点D,点E是AC的中点.
(1)试判断直线DE与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为2,∠B=50°,AC=6,求图中阴影部分的面积.
【答案】(1)直线DE与⊙O相切,见解析;(2)6-![]() π
π
【解析】
(1)连接OE、OD,根据切线的性质得到∠OAC=90°,根据三角形中位线定理得到OE∥BC,证明△AOE≌△DOE,根据全等三角形的性质、切线的判定定理证明;
(2)根据扇形的面积公式计算即可.
解:(1)直线DE与⊙O相切,
理由如下:连接OE、OD,如图,
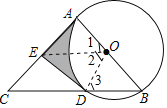
∵AC是⊙O的切线,
∴AB⊥AC,
∴∠OAC=90°,
∵点E是AC的中点,O点为AB的中点,
∴OE∥BC,
∴∠1=∠B,∠2=∠3,
∵OB=OD,
∴∠B=∠3,
∴∠1=∠2,
在△AOE和△DOE中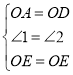 ,
,
∴△AOE≌△DOE(SAS)
∴∠ODE=∠OAE=90°,
∴DE⊥OD,
∵OD为⊙O的半径,
∴DE为⊙O的切线;
(2)∵DE、AE是⊙O的切线,
∴DE=AE,
∵点E是AC的中点,
∴AE=![]() AC=3,
AC=3,
∠AOD=2∠B=2×50°=100°,
∴图中阴影部分的面积=2×![]() ×2×3﹣
×2×3﹣![]() =6-
=6-![]() π.
π.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
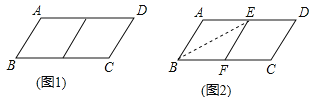
【题目】邻边不相等的平行四边形纸片,剪去一个菱形,余下一个四边形,称为第一次操作;在余下的四边形纸片中再剪去一个菱形,又余下一个四边形,称为第二次操作;……依次类推,若第n次操作余下的四边形是菱形,则称原平行四边形为n阶准菱形,如图1,平行四边形![]() 中,若
中,若![]() ,则平行四边形
,则平行四边形![]() 为1阶准菱形.
为1阶准菱形.
(1)判断与推理:
① 邻边长分别为2和3的平行四边形是__________阶准菱形;
② 小明为了剪去一个菱形,进行如下操作:如图2,把平行四边形![]() 沿着
沿着![]() 折叠(点
折叠(点![]() 在
在![]() 上)使点
上)使点![]() 落在
落在![]() 边上的点
边上的点![]() ,得到四边形
,得到四边形![]() ,请证明四边形
,请证明四边形![]() 是菱形.
是菱形.
(2)操作、探究与计算:
① 已知平行四边形![]() 的邻边分别为1,
的邻边分别为1,![]() 裁剪线的示意图,并在图形下方写出
裁剪线的示意图,并在图形下方写出![]() 的值;
的值;
② 已知平行四边形![]() 的邻边长分别为
的邻边长分别为![]() ,满足
,满足![]() ,请写出平行四边形
,请写出平行四边形![]() 是几阶准菱形.
是几阶准菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
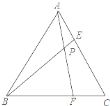
【题目】如图,等边三角形ABC的边长为![]() cm,在AC,BC边上各取一点E,F,使得AE=CF,连接AF,BE相交于点P.(1)则∠APB=______度;(2)当点E从点A运动到点C时,则动点P经过的路径长为________cm.
cm,在AC,BC边上各取一点E,F,使得AE=CF,连接AF,BE相交于点P.(1)则∠APB=______度;(2)当点E从点A运动到点C时,则动点P经过的路径长为________cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
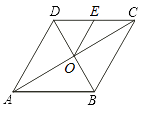
【题目】如图,菱形ABCD的对角线AC、BD相交于点O,点E为边CD的中点,若菱形ABCD的周长为16,∠BAD=60°,则△OCE的面积是( )
A. ![]() B. 2 C.
B. 2 C. ![]() D. 4
D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
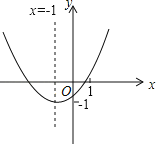
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为直线x=﹣1,与x轴的交点为(x1,0)、(x2,0),其中0<x1<1,有下列结论:①c>0;②﹣3<x2<﹣2;③a+b+c<0;④b2﹣4ac>0;⑤已知图象上点A(4,y1),B(1,y2),则y1>y2.其中,正确结论的个数有( )
A.5B.4C.3D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,D是BC边的中点,以D为顶点作一个120°的角,角的两边分别交直线AB,AC于M,N两点,以点D为中心旋转∠MDN(∠MDN的度数不变),若DM与AB垂直时(如图①所示),易证BM +CN =BD.
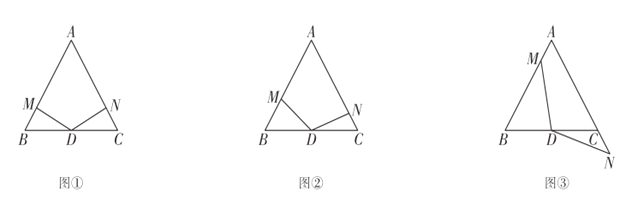
(1)如图②,若DM与AB不垂直时,点M在边AB上,点N在边AC上,上述结论是否成立?若成立,请给予证明;若不成立,请说明理由;
(2)如图③,若DM与AB不垂直时,点M在边AB.上,点N在边AC的延长线上,上述结论是否成立?若不成立,请写出BM,CN,BD之间的数量关系,不用证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从⊙O外一点A引⊙O的切线AB,切点为B,连接AO并延长交⊙O于点C,点D.连接BC.
(1)如图1,若∠A=26°,求∠C的度数;
(2)如图2,若AE平分∠BAC,交BC于点E.求∠AEB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
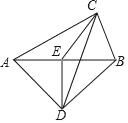
【题目】如图,把一副三角板按如图放置,∠ACB=∠ADB=90°,∠CAB=30°,∠DAB=45°,点E是AB的中点,连结CE,DE,DC.若AB=8,则△DEC的面积为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com