
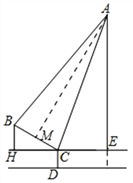
【题目】如图1,图2,分别是吊车在吊一物品时的实物图与示意图,已知吊车底盘CD的高度为1.8米,支架BC的长为4米,且与地面成30°角,吊绳AB与支架BC的夹角为80°,吊臂AC与地面成70°角,求吊车的吊臂顶端A点距地面的高度是多少米?(精确到0.1米,参考数据:sin10°=cos80°=0.17,cos10°=sin80°=0.98,sin20°=cos70°=0.34,tan70°=2.75,sin70°=0.94)

【答案】点A到地面的距离为12.9米.
【解析】试题分析:过点A作AM⊥BC于M,先证明∠ABC=∠ACB,推出AB=AC.在Rt△ACM中,求出AC,再在Rt△ACE中求出AE即可解决问题.
试题解析:解:由题可知,BH⊥HE,AE⊥HE,CD=2米,BC=4米,∠BCH=30°,∠ABC=80°,∠ACE=70°.∵∠BCH+∠ACB+∠ACE=180°,∴∠ACB=80°.
∵∠ABC=80°,∴∠ABC=∠ACB,∴AB=AC.
过点A作AM⊥BC于M,则CM=BM=2米.
∵在Rt△ACM中,CM=2米,∠ACB=80°,∴![]() =cos∠ACB=cos80°≈0.17,∴AC=
=cos∠ACB=cos80°≈0.17,∴AC=![]() =
=![]() (米).∵在Rt△ACE中,AC=
(米).∵在Rt△ACE中,AC=![]() ,∠ACE=70°,∴
,∠ACE=70°,∴![]() =sin∠ACE=sin70°≈0.94,
=sin∠ACE=sin70°≈0.94,
∴AE=![]() ×0.94=
×0.94=![]() ≈11.1(米),11.1+2=13.1(米)
≈11.1(米),11.1+2=13.1(米)
故点A到地面的高度为13.1米.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2﹣2x+3与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1关于点B的中心对称得C2,C2与x轴交于另一点C,将C2关于点C的中心对称得C3,连接C1与C3的顶点,则图中阴影部分的面积为_____.
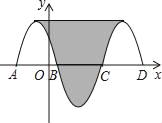
【答案】32
【解析】试题分析:∵抛物线y=﹣x2﹣2x+3与x轴交于点A、B,
∴当y=0时,则﹣x2﹣2x+3=0,
解得x=﹣3或x=1,
则A,B的坐标分别为(﹣3,0),(1,0),
AB的长度为4,
从C1,C3两个部分顶点分别向下作垂线交x轴于E、F两点.
根据中心对称的性质,x轴下方部分可以沿对称轴平均分成两部分补到C1与C2.
如图所示,阴影部分转化为矩形.
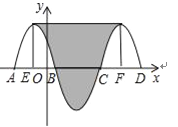
根据对称性,可得BE=CF=4÷2=2,则EF=8
利用配方法可得y=﹣x2﹣2x﹣3=﹣(x+1)2+4
则顶点坐标为(﹣1,4),即阴影部分的高为4,
S阴=8×4=32.
考点:抛物线与x轴的交点.
【题型】填空题
【结束】
17
【题目】解方程:(1)2(3x﹣1)=16;(2)![]() ;(3)
;(3)![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
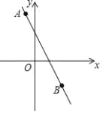
【题目】在直角坐标系中,一条直线经过A(﹣1,5),P(2,a),B(3,﹣3).
(1)求直线AB的函数表达式;
(2)求a的值;
(3)求△AOP的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,货轮O在航行过程中,发现灯塔A在它北偏东30°的方向上,海岛B在它南偏东60°方向上.则下列结论:
①∠NOA=30°;
②图中∠NOB的补角有两个,分别是∠SOB和∠EOA;
③图中有4对互余的角;
④货轮O在海岛B的西偏北30°的方向上.
其中正确结论的个数有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
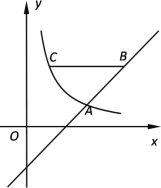
【题目】如图,在直角坐标系![]() 中,反比例函数图像与直线
中,反比例函数图像与直线![]() 相交于横坐标为3的点A.
相交于横坐标为3的点A.
(1)求反比例函数的解析式;
(2)如果点B在直线![]() 上,点C在反比例函数图像上,BC//
上,点C在反比例函数图像上,BC//![]() 轴,BC= 4,且BC在点A上方,求点B的坐标.
轴,BC= 4,且BC在点A上方,求点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
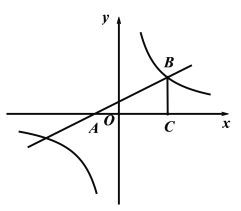
【题目】已知:如图,在平面直角坐标系xOy中,直线![]() 与x轴交于点A,在第一象限内与反比例函数图像交于点B,BC垂直于x轴,垂足为点C,且OC=2AO.求
与x轴交于点A,在第一象限内与反比例函数图像交于点B,BC垂直于x轴,垂足为点C,且OC=2AO.求
(1)点![]() 的坐标;
的坐标;
(2)反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在图1、图2中,线段AC=CE,点B是线段AC的中点,点D是线段CE的中点,四边形BCGF和CDHN都是正方形,AE的中点是M.如图1,点E在AC的延长线上,点N与点G重合时,点M与点C重合,容易证明FM=MH,FM⊥HM;现将图1的CE绕点C顺时针旋转一个锐角,得到图2,判断△FMH的形状,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着互联网的普及,某手机厂商采用先网络预定,然后根据订单量生产手机的方式销售,2015年该厂商将推出一款新手机,根据相关统计数据预测,定价为2200元,日预订量为20000台,若定价每减少100元,则日预订量增加10000台.
(1)设定价减少x元,预订量为y台,写出y与x的函数关系式;
(2)若每台手机的成本是1200元,求所获的利润w(元)与x(元)的函数关系式,并说明当定价为多少时所获利润最大;
(3)若手机加工厂每天最多加工50000台,且每批手机会有5%的故障率,通过计算说明每天最多接受的预订量为多少?按最大量接受预订时,每台售价多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com