
【题目】随着互联网的普及,某手机厂商采用先网络预定,然后根据订单量生产手机的方式销售,2015年该厂商将推出一款新手机,根据相关统计数据预测,定价为2200元,日预订量为20000台,若定价每减少100元,则日预订量增加10000台.
(1)设定价减少x元,预订量为y台,写出y与x的函数关系式;
(2)若每台手机的成本是1200元,求所获的利润w(元)与x(元)的函数关系式,并说明当定价为多少时所获利润最大;
(3)若手机加工厂每天最多加工50000台,且每批手机会有5%的故障率,通过计算说明每天最多接受的预订量为多少?按最大量接受预订时,每台售价多少元?
【答案】(1)y=100x+20000;(2)W=(2200﹣1200﹣x)(100x+20000),定价为1800元时,所获利润最大;(3)47500,1925.
【解析】试题分析:(1)根据题意列代数式即可;
(2)根据利润=单台利润×预订量,列出函数表达式,根据二次函数性质解决定价为多少时所获利润最大;
(3)根据题意列式计算每天最多接受的预订量,根据每天最多接受的预订量列方程求出最大量接受预订时每台售价即可.
试题解析:解:(1)根据题意:y=20000+![]() ×10000=100x+20000;
×10000=100x+20000;
(2)设所获的利润w(元),则W=(2200﹣1200﹣x)(100x+20000)
=﹣100(x﹣400)2+36000000;
所以当降价400元,即定价为2200﹣400=1800元时,所获利润最大;
(2)根据题意每天最多接受50000(1﹣0.05)=47500台,此时47500=100x+20000,解得:x=275.
所以最大量接受预订时,每台定价2200﹣275=1925元.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在等腰三角形ABC中,AB=AC,以底边BC的垂直平分线和BC所在的直线建立平面直角坐标系,抛物线y=﹣![]() x2+
x2+![]() x+4经过A、B两点.
x+4经过A、B两点.

(1)写出点A、点B的坐标;
(2)若一条与y轴重合的直线l以每秒2个单位长度的速度向右平移,分别交线段OA、CA和抛物线于点E、M和点P,连接PA、PB.设直线l移动的时间为t(0<t<4)秒,求四边形PBCA的面积S(面积单位)与t(秒)的函数关系式,并求出四边形PBCA的最大面积;
(3)在(2)的条件下,是否存在t,使得△PAM是直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解“阳光体育”活动的开展情况,从全校2000名学生中,随机抽取部分学生进行问卷调查(每名学生只能填写一项自己喜欢的活动项目),并将调查结果绘制成如下两幅不完整的统计图.
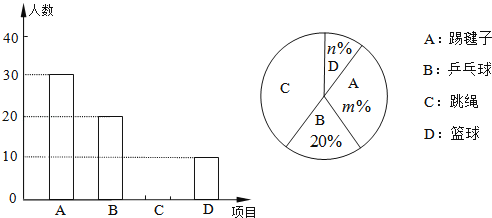
根据以上信息,解答下列问题:
(1)被调查的学生共有 人,并补全条形统计图;
(2)在扇形统计图中,m= ,n= ,表示区域C的圆心角为 度;
(3)全校学生中喜欢篮球的人数大约有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上![]() 点表示数
点表示数![]() ,
,![]() 点表示数
点表示数![]() ,
,![]() 表示
表示![]() 点和
点和![]() 点之间的距离,且
点之间的距离,且![]() ,
,![]() 满足
满足![]() .
.
![]()
(1)求![]() ,
,![]() 两点之间的距离;
两点之间的距离;
(2)若在数轴上存在一点![]() ,且
,且![]() ,直接写出
,直接写出![]() 点表示的数;
点表示的数;
(3)若在原点![]() 处放一挡板,一小球甲从点
处放一挡板,一小球甲从点![]() 处以1个单位/秒的速度向左运动;同时另一小球乙从点
处以1个单位/秒的速度向左运动;同时另一小球乙从点![]() 处以2个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为t(秒),
处以2个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为t(秒),
①分别表示甲、乙两小球到原点的距离(用t表示);
②求甲、乙两小球到原点的距离相等时经历的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD中,F是AB上一点,H是BC延长线上一点,连接FH,将△FBH沿FH翻折,使点B的对应点E落在AD上,EH与CD交于点G,连接BG交FH于点M,当GB平分∠CGE时,BM=2![]() ,AE=8,则ED=______.
,AE=8,则ED=______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某综合实践小组的同学对本校八年级学生课外阅读最喜爱的图书种类进行了调查.
(1)该综合实践小组设计了下列的调查方式,比较合理的是 (填写序号即可)
A.对八年级各班的数学课代表进行问卷调查
B.对八年级(1)班的全班同学进行问卷调查
C.对八年级各班学号为![]() 的倍数的同学进行问卷调查
的倍数的同学进行问卷调查
(2)小组同学根据问卷调查(每个被调查的学生只能选择其中一项)的结果绘制了如下两幅统计图(不完整):
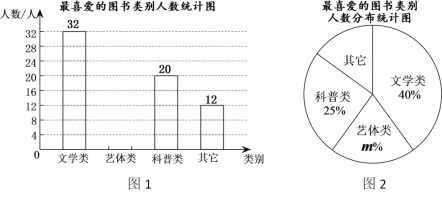
根据以上信息,回答下列问题:
①这次被调查的学生共有 人;
②请将图1补充完整并在图上标出数据;
③图2中,![]() ,“科普类”部分扇形的圆心角是
,“科普类”部分扇形的圆心角是 ![]() ;
;
④若该校八年级共有学生![]() 人,根据调查结果估计此年级最喜欢“文学类”图书的学生约有 人.
人,根据调查结果估计此年级最喜欢“文学类”图书的学生约有 人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点![]() 在线段
在线段![]() 上,
上,![]() .
.
(1) 如图1,![]() ,
,![]() 两点同时从
两点同时从![]() ,
,![]() 出发,分别以
出发,分别以![]() ,
,![]() 的速度沿直线
的速度沿直线![]() 向左运动;
向左运动;
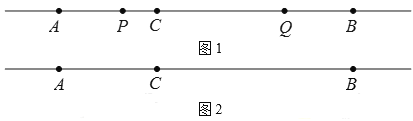
①在![]() 还未到达
还未到达![]() 点时,
点时,![]() 的值为 ;
的值为 ;
②当![]() 在
在![]() 右侧时(点
右侧时(点![]() 与
与![]() 不重合),取
不重合),取![]() 中点
中点![]() ,
,![]() 的中点是
的中点是![]() ,求
,求![]() 的值;
的值;
(2) 若![]() 是直线
是直线![]() 上一点,且
上一点,且![]() .则
.则![]() 的值为 .
的值为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 两点分别是
两点分别是![]() 轴和
轴和![]() 轴正半轴上两个动点,以三点
轴正半轴上两个动点,以三点![]() 为顶点的矩形
为顶点的矩形![]() 的面积为24,反比例函数
的面积为24,反比例函数![]() (
(![]() 为常数且
为常数且![]() )的图象与矩形
)的图象与矩形![]() 的两边
的两边![]() 分别交于点
分别交于点![]() .
.
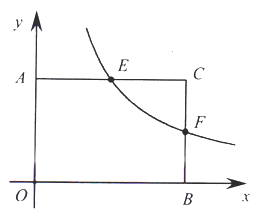
(1)若![]() 且点
且点![]() 的横坐标为3.
的横坐标为3.
①点![]() 的坐标为 ,点
的坐标为 ,点![]() 的坐标为 (不需写过程,直接写出结果);
的坐标为 (不需写过程,直接写出结果);
②在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 的周长最小?若存在,请求出
的周长最小?若存在,请求出![]() 的周长最小值;若不存在,请说明理由.
的周长最小值;若不存在,请说明理由.
(2)连接![]() ,在点
,在点![]() 的运动过程中,
的运动过程中,![]() 的面积会发生变化吗?若变化,请说明理由,若不变,请用含
的面积会发生变化吗?若变化,请说明理由,若不变,请用含![]() 的代数式表示出
的代数式表示出![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义一种对正整数n的“F”运算:①当n为奇数时,F(n)=3n+1;②当n为偶数时,F(n)=![]() (其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=24,则:若n=13,则第2018次“F”运算的结果是_____.
(其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=24,则:若n=13,则第2018次“F”运算的结果是_____.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com