
【题目】定义一种对正整数n的“F”运算:①当n为奇数时,F(n)=3n+1;②当n为偶数时,F(n)=![]() (其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=24,则:若n=13,则第2018次“F”运算的结果是_____.
(其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=24,则:若n=13,则第2018次“F”运算的结果是_____.
![]()
科目:初中数学 来源: 题型:
【题目】随着互联网的普及,某手机厂商采用先网络预定,然后根据订单量生产手机的方式销售,2015年该厂商将推出一款新手机,根据相关统计数据预测,定价为2200元,日预订量为20000台,若定价每减少100元,则日预订量增加10000台.
(1)设定价减少x元,预订量为y台,写出y与x的函数关系式;
(2)若每台手机的成本是1200元,求所获的利润w(元)与x(元)的函数关系式,并说明当定价为多少时所获利润最大;
(3)若手机加工厂每天最多加工50000台,且每批手机会有5%的故障率,通过计算说明每天最多接受的预订量为多少?按最大量接受预订时,每台售价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
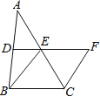
【题目】图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到F,使得EF=BE,连接CF.
(1)求证:四边形BCFE是菱形.
(2)若DE=4cm,∠EBC=60°,求菱形BCFE的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“元旦”期间,某文具店购进100只两种型号的文具进行销售,其进价和售价如下
型号 | 进价(元/只) | 售价(元/只) |
A型 | 10 | 12 |
B型 | 15 | 23 |
(1)该店用1300元可以购进A,B两种型号的文具各多少只?
(2)若把所购进A,B两种型号的文具全部销售完,利润率超过40%没有?请你说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D为AB边上一点,E为CD中点,AC=![]() ,∠ABC=30°,∠A=∠BED=45°,则BD的长为( )
,∠ABC=30°,∠A=∠BED=45°,则BD的长为( )

A. ![]() B.
B. ![]() +1﹣
+1﹣![]() C.
C. ![]() ﹣
﹣![]() D.
D. ![]() ﹣1
﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
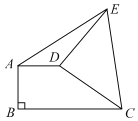
【题目】如图 ,直角梯形 ABCD 中, AD ∥ BC , AB ⊥ BC,AD 2 ,将腰CD 以点 D 为中心逆时针旋转 90°至 DE ,连接 AE、CE ,△ADE 的面积为 3,则 BC 的长为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有三个有理数x,y,z,若x=![]() ,且x与y互为相反数,y是z的倒数.
,且x与y互为相反数,y是z的倒数.
(1)当n为奇数时,你能求出x,y,z这三个数吗?当n为偶数时,你能求出x,y,z,这三个数吗?若能,请计算并写出结果;若不能,请说明理由.
(2)根据(1)的结果计算:xy﹣yn﹣(y﹣z)2019的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
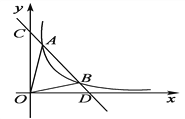
【题目】如图,一次函数y=kx+b与反比例函数y=![]() (x>0)的图象交于A(m,6),B(3,n)两点.
(x>0)的图象交于A(m,6),B(3,n)两点.
(1)求一次函数的解析式;
(2)根据图象直接写出kx+b-![]() <0时x的取值范围;
<0时x的取值范围;
(3)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为民中学租用两辆速度相同的小汽车送1名带队老师和6名学生到城区中学参加数学竞赛,每辆限坐4人(不包括司机).其中一辆小汽车在距离考场16.5 km的地方出现故障,此时离截止进考场的时刻还有50分钟,这时唯一可利用的交通工具是另一辆小汽车,且这辆车的平均速度是55 km/h,人步行的速度是5 km/h(上、下车时间忽略不计).
(1)若小汽车送4人到达考场,然后再回到出故障处接其他人,请你通过计算说明他们能否在截止进考场的时刻前到达考场;
(2)假如你是带队的老师,请设计一种你认为较优的运送方案,使他们能在截止进考场的时刻前到达考场,并通过计算说明方案的可行性.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com