
【题目】某校为了解“阳光体育”活动的开展情况,从全校2000名学生中,随机抽取部分学生进行问卷调查(每名学生只能填写一项自己喜欢的活动项目),并将调查结果绘制成如下两幅不完整的统计图.
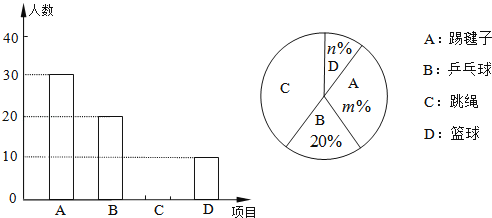
根据以上信息,解答下列问题:
(1)被调查的学生共有 人,并补全条形统计图;
(2)在扇形统计图中,m= ,n= ,表示区域C的圆心角为 度;
(3)全校学生中喜欢篮球的人数大约有多少?
【答案】(1)学生总数100人,跳绳40人,条形统计图见解析;(2)144°;(3)200人.
【解析】
(1)用B组频数除以其所占的百分比即可求得样本容量;
(2)用A组人数除以总人数即可求得m值,用D组人数除以总人数即可求得n值;
(3)用总人数乘以D类所占的百分比即可求得全校喜欢篮球的人数;
解:(1)观察统计图知:喜欢乒乓球的有20人,占20%,
故被调查的学生总数有20÷20%=100人,
喜欢跳绳的有100﹣30﹣20﹣10=40人,
条形统计图为:
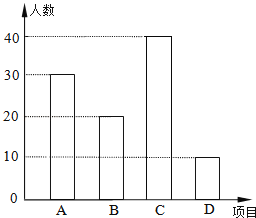
(2)∵A组有30人,D组有10人,共有100人,
∴A组所占的百分比为:30%,D组所占的百分比为10%,
∴m=30,n=10;
表示区域C的圆心角为![]() ×360°=144°;
×360°=144°;
(3)∵全校共有2000人,喜欢篮球的占10%,
∴喜欢篮球的有2000×10%=200人.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公大楼顶端A测得旗杆顶端E的俯角α是45°,旗杆低端D到大楼前梯砍底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:![]() ,则大楼AB的高度为_________米.
,则大楼AB的高度为_________米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为2的正方形纸片ABCD中,点M为边CD上一点(不与C,D重合),将△ADM沿AM折叠得到△AME,延长ME交边BC于点N,连结AN.
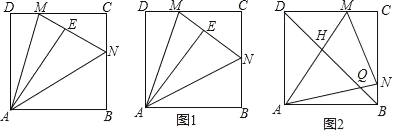
(1)猜想∠MAN的大小是否变化,并说明理由;
(2)如图1,当N点恰为BC中点时,求DM的长度;
(3)如图2,连结BD,分别交AN,AM于点Q,H.若BQ=![]() ,求线段QH的长度.
,求线段QH的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
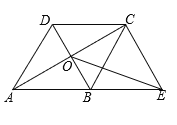
【题目】在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE∥DB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若∠DAB=60°,且AB=4,求OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 请阅读下列材料,并解答相应的问题:
将若干个数组成一个正方形数阵,若任意一行,一列及对角线上的数字之和都相等,则称具有这种性质的数字方阵为“幻方”中国古代称“幻方”为“河图“、“洛书“等,例如,下面是三个三阶幻方,是将数字1,2,3,4,5,6,7,8,9填入到3×3的方格中得到的,其每行、每列、每条对角线上的三个数之和相等.
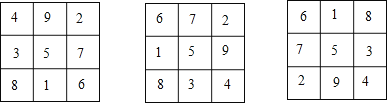
(1)设图1的三阶幻方中间的数字是x,用x的代数式表示幻方中9个数的和为 ;
(2)请你将下列九个数:﹣10、﹣8、﹣6、﹣4、﹣2、0、2、4、6分别填入图2方格中,使得每行、每列、每条对角线上的三个数之和都相等;
(3)图3是一个三阶幻方,那么标有x的方格中所填的数是 ;
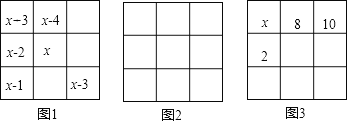
(4)如图4所示的每一个圆中分别填写了1、2、3…19中的一个数字(不同的圆中填写的数字各不相同),使得图中每一个横或斜方向的线段上几个圆内的数之和都相等,现在已知该图中七个圆内的数字,则图中的x= ,y= .

查看答案和解析>>
科目:初中数学 来源: 题型:
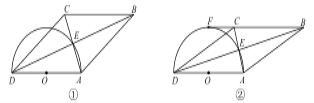
【题目】四边形 ABCD 的对角线交于点 E,且 AE=EC,BE=ED,以 AD 为直径的半圆过点 E,圆心 为 O.
(1)如图①,求证:四边形 ABCD 为菱形;
(2)如图②,若 BC 的延长线与半圆相切于点 F,且直径 AD=6,求弧AE 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着互联网的普及,某手机厂商采用先网络预定,然后根据订单量生产手机的方式销售,2015年该厂商将推出一款新手机,根据相关统计数据预测,定价为2200元,日预订量为20000台,若定价每减少100元,则日预订量增加10000台.
(1)设定价减少x元,预订量为y台,写出y与x的函数关系式;
(2)若每台手机的成本是1200元,求所获的利润w(元)与x(元)的函数关系式,并说明当定价为多少时所获利润最大;
(3)若手机加工厂每天最多加工50000台,且每批手机会有5%的故障率,通过计算说明每天最多接受的预订量为多少?按最大量接受预订时,每台售价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
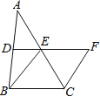
【题目】图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到F,使得EF=BE,连接CF.
(1)求证:四边形BCFE是菱形.
(2)若DE=4cm,∠EBC=60°,求菱形BCFE的面积。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com