
【题目】如图,边长为2的正方形纸片ABCD中,点M为边CD上一点(不与C,D重合),将△ADM沿AM折叠得到△AME,延长ME交边BC于点N,连结AN.
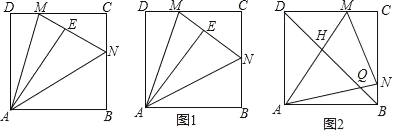
(1)猜想∠MAN的大小是否变化,并说明理由;
(2)如图1,当N点恰为BC中点时,求DM的长度;
(3)如图2,连结BD,分别交AN,AM于点Q,H.若BQ=![]() ,求线段QH的长度.
,求线段QH的长度.
【答案】(1)∠MAN的大小没有变化,理由见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)由折叠知AD=AE、DM=EM、∠D=∠AEM=90°、∠DAM=∠EAM=![]() ∠DAE,再证Rt△BAN≌Rt△EAN得∠BAN=∠EAN=
∠DAE,再证Rt△BAN≌Rt△EAN得∠BAN=∠EAN=![]() ∠BAE,根据∠MAN=∠EAM+∠EAN=
∠BAE,根据∠MAN=∠EAM+∠EAN=![]() (∠DAE+∠BAE)可得答案;
(∠DAE+∠BAE)可得答案;
(2)由题意知EN=BN=CN=1,设DM=EM=x,则MC=2-x、MN=1+x,在Rt△MNC中,由MC2+CN2=MN2列出关于x的方程求解可得;
(3)将△ABQ绕点A逆时针旋转90°得△ADG,连接GH,由旋转知DG=BQ=![]() ,AG=AQ,∠ADG=∠ABQ=∠ADB=45°,∠BAQ=∠DAG,证△GAH≌△QAH得GH=QH,设GH=QH=a,得BD=
,AG=AQ,∠ADG=∠ABQ=∠ADB=45°,∠BAQ=∠DAG,证△GAH≌△QAH得GH=QH,设GH=QH=a,得BD=![]() AB=2
AB=2![]() ,BQ=
,BQ=![]() ,DQ=
,DQ=![]() ,DH=
,DH=![]() -a,在Rt△DGH中,由DG2+DH2=GH2可得关于a的方程,解之可得答案.
-a,在Rt△DGH中,由DG2+DH2=GH2可得关于a的方程,解之可得答案.
(1)∠MAN的大小没有变化,
∵将△ADM沿AM折叠得到△AME,
∴△ADM≌△AEM,
∴AD=AE=2、DM=EM、∠D=∠AEM=90°、∠DAM=∠EAM=![]() ∠DAE,
∠DAE,
又∵AD=AB=2、∠D=∠B=90°,
∴AE=AB、∠B=∠AEM=∠AEN=90°,
在Rt△BAN和Rt△EAN中,
∵![]() ,
,
∴Rt△BAN≌Rt△EAN(HL),
∴∠BAN=∠EAN=![]() ∠BAE,
∠BAE,
则∠MAN=∠EAM+∠EAN=![]() ∠DAE+
∠DAE+![]() ∠BAE=
∠BAE=![]() (∠DAE+∠BAE)=
(∠DAE+∠BAE)=![]() ∠BAD=45°,
∠BAD=45°,
∴∠MAN的大小没有变化;
(2)∵N点恰为BC中点,
∴EN=BN=CN=1,
设DM=EM=x,则MC=2﹣x,
∴MN=ME+EN=1+x,
在Rt△MNC中,由MC2+CN2=MN2可得(2﹣x)2+12=(1+x)2,
解得:x=![]() ,即DM=
,即DM=![]() ;
;
(3)如图,将△ABQ绕点A逆时针旋转90°得△ADG,连接GH,
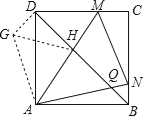
则△ABQ≌△ADG,
∴DG=BQ=![]() 、AG=AQ、∠ADG=∠ABQ=∠ADB=45°、∠BAQ=∠DAG,
、AG=AQ、∠ADG=∠ABQ=∠ADB=45°、∠BAQ=∠DAG,
∵∠MAN=![]() ∠BAD=45°,
∠BAD=45°,
∴∠BAQ+∠DAM=∠DAG+∠DAM=∠GAH=45°,
则∠GAH=∠QAH,
在△GAH和△QAH中,
∵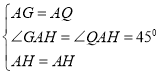 ,
,
∴△GAH≌△QAH(SAS),
∴GH=QH,
设GH=QH=a,
∵BD=![]() AB=2
AB=2![]() ,BQ=
,BQ=![]() ,
,
∴DQ=BD﹣BQ=![]() ,
,
∴DH=![]() ﹣a,
﹣a,
∵∠ADG=∠ADH=45°,
∴∠GDH=90°,
在Rt△DGH中,由DG2+DH2=GH2可得(![]() )2+(
)2+(![]() ﹣a)2=a2,
﹣a)2=a2,
解得:a=![]() ,即QH=
,即QH=![]() .
.


科目:初中数学 来源: 题型:
【题目】
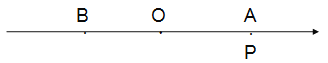
(1)写出数轴上点B表示的数 _______,点P表示的数________(用含t的代数式表示);
(2)动点Q从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发,问点P运动多少秒时追上点Q?(5分)
(3)若M为AP的中点,N为PB的中点.点P在运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请你画出图形,并求出线段MN的长;(5分)
(4)若点D是数轴上一点,点D表示的数是x,请你探索式子|x+6|+|x-8|是否有最小值?如果有,直接写出最小值;如果没有,说明理由.(5分)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰三角形ABC中,AB=AC,以底边BC的垂直平分线和BC所在的直线建立平面直角坐标系,抛物线y=﹣![]() x2+
x2+![]() x+4经过A、B两点.
x+4经过A、B两点.

(1)写出点A、点B的坐标;
(2)若一条与y轴重合的直线l以每秒2个单位长度的速度向右平移,分别交线段OA、CA和抛物线于点E、M和点P,连接PA、PB.设直线l移动的时间为t(0<t<4)秒,求四边形PBCA的面积S(面积单位)与t(秒)的函数关系式,并求出四边形PBCA的最大面积;
(3)在(2)的条件下,是否存在t,使得△PAM是直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC中,AB=AC=5cm,BC=8cm,动点N从点C出发,沿线段CB以2cm/s的速度向点B运动,并在达到点B后,立即以同样的速度返回向点C运动;同时动点M从点B出发,沿折线B﹣A﹣C以1cm/s的速度向点C运动,当点N回到点C时,两个动点同时停止运动.⊙M是以M为圆心,1cm为半径的圆,设运动时间为t(s) (t>0)
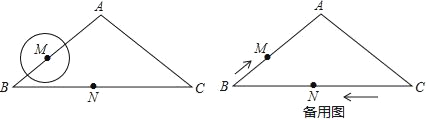
(1)tanB= ;
(2)当点M在线段AB上运动,且⊙M与BC相切时,求t的值;
(3)当t为何值时,⊙M与折线B﹣A﹣C的两个交点在等腰三角形ABC对称轴的同侧,且经过交点和点N的直线与⊙M相切?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解本校八年级学生生物考试测试情况,随机抽取了本校八年级部分学生的生物测试成绩为样本,按A(优秀)、B(良好)、C(合格)、D(不合格)四个等级进行统计,并将统计结果绘制成如下统计图表.请你结合图表中所给信息解答下列问题:
等级 | 人数 |
A(优秀) | 40 |
B(良好) | 80 |
C(合格) | 70 |
D(不合格) |
(1)请将上面表格中缺少的数据补充完整;
(2)扇形统计图中“A”部分所对应的圆心角的度数是 ;
(3)该校八年级共有1200名学生参加了身体素质测试,试估计测试成绩合格以上(含合格)的人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解“阳光体育”活动的开展情况,从全校2000名学生中,随机抽取部分学生进行问卷调查(每名学生只能填写一项自己喜欢的活动项目),并将调查结果绘制成如下两幅不完整的统计图.
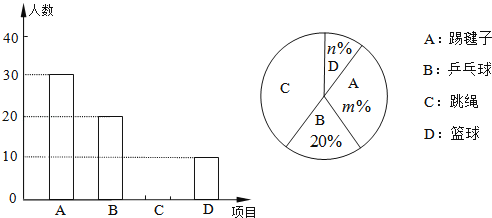
根据以上信息,解答下列问题:
(1)被调查的学生共有 人,并补全条形统计图;
(2)在扇形统计图中,m= ,n= ,表示区域C的圆心角为 度;
(3)全校学生中喜欢篮球的人数大约有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上![]() 点表示数
点表示数![]() ,
,![]() 点表示数
点表示数![]() ,
,![]() 表示
表示![]() 点和
点和![]() 点之间的距离,且
点之间的距离,且![]() ,
,![]() 满足
满足![]() .
.
![]()
(1)求![]() ,
,![]() 两点之间的距离;
两点之间的距离;
(2)若在数轴上存在一点![]() ,且
,且![]() ,直接写出
,直接写出![]() 点表示的数;
点表示的数;
(3)若在原点![]() 处放一挡板,一小球甲从点
处放一挡板,一小球甲从点![]() 处以1个单位/秒的速度向左运动;同时另一小球乙从点
处以1个单位/秒的速度向左运动;同时另一小球乙从点![]() 处以2个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为t(秒),
处以2个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为t(秒),
①分别表示甲、乙两小球到原点的距离(用t表示);
②求甲、乙两小球到原点的距离相等时经历的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 两点分别是
两点分别是![]() 轴和
轴和![]() 轴正半轴上两个动点,以三点
轴正半轴上两个动点,以三点![]() 为顶点的矩形
为顶点的矩形![]() 的面积为24,反比例函数
的面积为24,反比例函数![]() (
(![]() 为常数且
为常数且![]() )的图象与矩形
)的图象与矩形![]() 的两边
的两边![]() 分别交于点
分别交于点![]() .
.
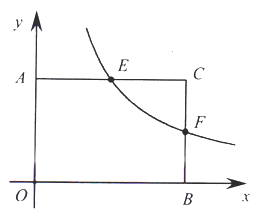
(1)若![]() 且点
且点![]() 的横坐标为3.
的横坐标为3.
①点![]() 的坐标为 ,点
的坐标为 ,点![]() 的坐标为 (不需写过程,直接写出结果);
的坐标为 (不需写过程,直接写出结果);
②在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 的周长最小?若存在,请求出
的周长最小?若存在,请求出![]() 的周长最小值;若不存在,请说明理由.
的周长最小值;若不存在,请说明理由.
(2)连接![]() ,在点
,在点![]() 的运动过程中,
的运动过程中,![]() 的面积会发生变化吗?若变化,请说明理由,若不变,请用含
的面积会发生变化吗?若变化,请说明理由,若不变,请用含![]() 的代数式表示出
的代数式表示出![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com