
【题目】如图,等腰三角形ABC中,AB=AC=5cm,BC=8cm,动点N从点C出发,沿线段CB以2cm/s的速度向点B运动,并在达到点B后,立即以同样的速度返回向点C运动;同时动点M从点B出发,沿折线B﹣A﹣C以1cm/s的速度向点C运动,当点N回到点C时,两个动点同时停止运动.⊙M是以M为圆心,1cm为半径的圆,设运动时间为t(s) (t>0)
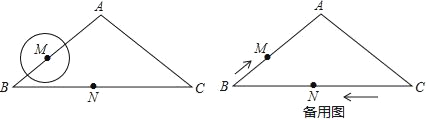
(1)tanB= ;
(2)当点M在线段AB上运动,且⊙M与BC相切时,求t的值;
(3)当t为何值时,⊙M与折线B﹣A﹣C的两个交点在等腰三角形ABC对称轴的同侧,且经过交点和点N的直线与⊙M相切?
【答案】(1)![]() ;(2)t=
;(2)t=![]() ;(3)满足条件的t的值为
;(3)满足条件的t的值为![]() s或
s或![]() s或
s或![]() s.
s.
【解析】试题分析:(1)作AH⊥BC用H,根据等腰三角形的性质以及勾股定理分别求得BH、AH的长,再利用正切的定义即可求得;
(2)作MK⊥BC于K,根据⊙M与BC相切,则可得MK=1,再根据sinB=![]() ,即可得;
,即可得;
(3)分0<t≤4, 4<t≤8,进行讨论即可得
试题解析:(1)如图1中,作AH⊥BC用H.
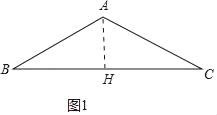
∵AB=AC=5,AH⊥BC,
∴BH=CH=![]() BC=4,AH=
BC=4,AH=![]() =3,
=3,
∴tanB=![]() ,
,
故答案为: ![]() ;
;
(2)如图2中,作MK⊥BC于K,
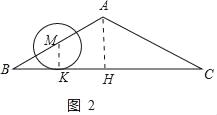
∵⊙M与BC相切,
∴MK=1,
∵sinB=![]() ,
,
∴BM=![]() ,
,
∴t=![]() s时,⊙M与BC相切;
s时,⊙M与BC相切;
(3)如图设⊙M交AB于P、G,连接GN,
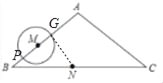
①当0<t≤4时,如果NG是⊙M的切线,则GN⊥AB,则有cosB=![]() ,
,
∴![]() ,
,
解得:t=![]() ,
,
②当PN是切线时,同法可得, ![]() ,
,
解得t=![]() .
.
③当4<t≤8时,同法可得, ![]() 或
或![]() ,
,
解得t=3(不合题意舍弃)或t=![]() ,
,
综上所述,满足条件的t的值为![]() s或
s或![]() s或
s或![]() s.
s.


 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源: 题型:
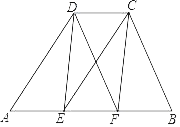
【题目】已知:如图,在四边形ABCD中,AB=3CD,AB∥CD,CE∥DA,DF∥CB.
(1)求证:四边形CDEF是平行四边形;
(2)填空:
①当四边形ABCD满足条件 时(仅需一个条件),四边形CDEF是矩形;
②当四边形ABCD满足条件 时(仅需一个条件),四边形CDEF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,正比例函数y=x的图象与一次函数y=kx﹣k的图象的交点坐标为A(m,2).
(1)求m的值和一次函数的解析式;
(2)设一次函数y=kx﹣k的图象与y轴交于点B,求△AOB的面积;
(3)直接写出使函数y=kx﹣k的值大于函数y=x的值的自变量x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公大楼顶端A测得旗杆顶端E的俯角α是45°,旗杆低端D到大楼前梯砍底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:![]() ,则大楼AB的高度为_________米.
,则大楼AB的高度为_________米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】己知:矩形ABCD的两边AB,BC的长是关于x的方程x2﹣mx+![]() =0的两个实数根.
=0的两个实数根.
(1)当m为何值时,矩形ABCD是正方形?求出这时正方形的边长;
(2)若AB的长为2,那么矩形ABCD的周长是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为2的正方形纸片ABCD中,点M为边CD上一点(不与C,D重合),将△ADM沿AM折叠得到△AME,延长ME交边BC于点N,连结AN.
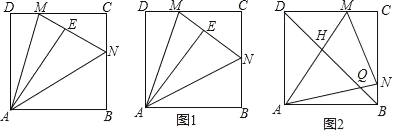
(1)猜想∠MAN的大小是否变化,并说明理由;
(2)如图1,当N点恰为BC中点时,求DM的长度;
(3)如图2,连结BD,分别交AN,AM于点Q,H.若BQ=![]() ,求线段QH的长度.
,求线段QH的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
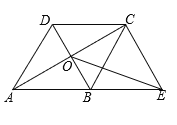
【题目】在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE∥DB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若∠DAB=60°,且AB=4,求OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
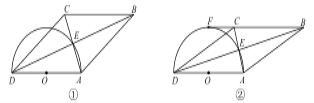
【题目】四边形 ABCD 的对角线交于点 E,且 AE=EC,BE=ED,以 AD 为直径的半圆过点 E,圆心 为 O.
(1)如图①,求证:四边形 ABCD 为菱形;
(2)如图②,若 BC 的延长线与半圆相切于点 F,且直径 AD=6,求弧AE 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分6分)某公司调查某中学学生对其环保产品的了解情况,随机抽取该校部分学生进行问卷,结果分“非常了解”、“比较了解”、“一般了解”、“不了解”四种类型,分别记为A、B、C、D.根据调查结果绘制了如下尚不完整的统计图. 
(1)本次问卷共随机调查了 名学生,扇形统计图中m= .
(2)请根据数据信息补全条形统计图;
(3)若该校有1000名学生,估计选择“非常了解”、“比较了解”共约有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com