
【题目】已知:如图,在四边形ABCD中,AB=3CD,AB∥CD,CE∥DA,DF∥CB.
(1)求证:四边形CDEF是平行四边形;
(2)填空:
①当四边形ABCD满足条件 时(仅需一个条件),四边形CDEF是矩形;
②当四边形ABCD满足条件 时(仅需一个条件),四边形CDEF是菱形.
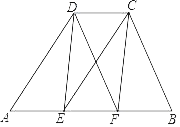
【答案】(1)详见解析;(2)①AD=BC;②AD⊥BC.
【解析】
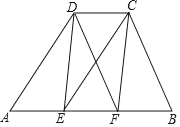
(1)利用两组对边分别平行的四边形是平行四边形,可得四边形AECD和四边形BFDC都是平行四边形,再由一组对边平行且相等的四边形是平行四边形可得CDEF是平行四边形.(2)①当AD=BC时,四边形EFCD是矩形.理由是:对角线相等的平行四边形是矩形;②当AD⊥BC时,四边形EFCD是菱形.理由是:对角线互相垂直的平行四边形是菱形.
解:
(1)证明:∵AB∥CD,CE∥AD,DF∥BC,
∴四边形AECD和四边形BFDC都是平行四边形,
∴AE=CD=FB,
∵AB=3CD,
∴EF=CD,
∴四边形CDEF是平行四边形.
(2)解:①当AD=BC时,四边形EFCD是矩形.
理由:∵四边形AECD和四边形BFDC都是平行四边形,
∴EC=AD,DF=BC,
∴EC=DF,
∵四边形EFDC是平行四边形,
∴四边形EFDC是矩形.
②当AD⊥BC时,四边形EFCD是菱形.
理由:∵AD∥CE,DF∥CB,AD⊥BC,
∴DF⊥EC,
∵四边形EFCD是平行四边形,
∴四边形EFCD是菱形.
故答案为AD=BC,AD⊥BC.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:
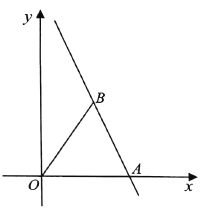
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是该直线上一点,满足
是该直线上一点,满足![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)若点![]() 是直线上另外一点,满足
是直线上另外一点,满足![]() ,且四边形
,且四边形![]() 是平行四边形,试画出符合要求的大致图形,并求出点
是平行四边形,试画出符合要求的大致图形,并求出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
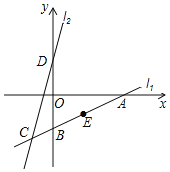
【题目】如图,直线l1:y=![]() x-4分别与x轴,y轴交于A,B两点,与直线l2交于点C(-2,m).点D是直线l2与y轴的交点,将点A向上平移3个单位,再向左平移8个单位恰好能与点D重合.
x-4分别与x轴,y轴交于A,B两点,与直线l2交于点C(-2,m).点D是直线l2与y轴的交点,将点A向上平移3个单位,再向左平移8个单位恰好能与点D重合.
(1)求直线l2的解析式;
(2)已知点E(n,-2)是直线l1上一点,将直线l2沿x轴向右平移.在平移过程中,当直线l2与线段BE有交点时,求平移距离d的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游泳馆普通票价20元/张,暑假为了促销,新推出两种优惠卡:
①金卡售价600元/张,每次凭卡不再收费.
②银卡售价150元/张,每次凭卡另收10元.
暑假普通票正常出售,两种优惠卡仅限暑假使用,不限次数.设游泳x次时,所需总费用为y元.

(1)分别写出选择银卡、普通票消费时,y与x之间的函数关系式;
(2)在同一坐标系中,若三种消费方式对应的函数图象如图所示,请求出点A、B、C的坐标;
(3)请根据函数图象,直接写出选择哪种消费方式更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
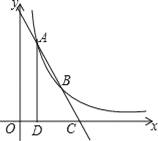
【题目】如图,点A(1,4)、B(2,a)在函数y=![]() (x>0)的图象上,直线AB与x轴相交于点C,AD⊥x轴于点D.
(x>0)的图象上,直线AB与x轴相交于点C,AD⊥x轴于点D.
(1)m= ;
(2)求点C的坐标;
(3)在x轴上是否存在点E,使以A、B、E为顶点的三角形与△ACD相似?若存在,求出点E的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
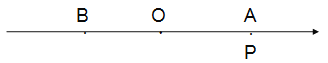
(1)写出数轴上点B表示的数 _______,点P表示的数________(用含t的代数式表示);
(2)动点Q从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发,问点P运动多少秒时追上点Q?(5分)
(3)若M为AP的中点,N为PB的中点.点P在运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请你画出图形,并求出线段MN的长;(5分)
(4)若点D是数轴上一点,点D表示的数是x,请你探索式子|x+6|+|x-8|是否有最小值?如果有,直接写出最小值;如果没有,说明理由.(5分)
查看答案和解析>>
科目:初中数学 来源: 题型:
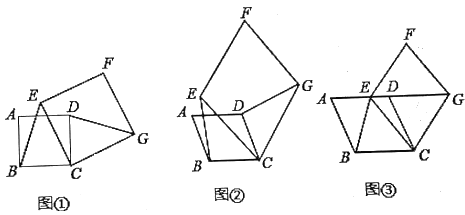
【题目】(1)(感知)如图①,四边形![]() 、
、![]() 均为正方形.
均为正方形.![]() 与
与![]() 的数量关系为________;
的数量关系为________;
(2)(拓展)如图②,四边形![]() 、
、![]() 均为菱形,且
均为菱形,且![]() .请判断
.请判断![]() 与
与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
(3)(应用)如图③,四边形![]() 、
、![]() 均为菱形,点
均为菱形,点![]() 在边
在边![]() 上,点
上,点![]() 在
在![]() 延长线上.若
延长线上.若![]() ,
,![]() ,
,![]() 的面积为9,则菱形
的面积为9,则菱形![]() 的面积为_______.
的面积为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上的A1,A2,A3,A4,……A20,这20个点所表示的数分别是a1,a2,a3,a4,……a20.若A1A2=A2A3=……=A19A20,且a3=20,|a1﹣a4|=12.
![]()
(1)线段A3A4的长度= ;a2= ;
(2)若|a1﹣x|=a2+a4,求x的值;
(3)线段MN从O点出发向右运动,当线段MN与线段A1A20开始有重叠部分到完全没有重叠部分经历了9秒.若线段MN=5,求线段MN的运动速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC中,AB=AC=5cm,BC=8cm,动点N从点C出发,沿线段CB以2cm/s的速度向点B运动,并在达到点B后,立即以同样的速度返回向点C运动;同时动点M从点B出发,沿折线B﹣A﹣C以1cm/s的速度向点C运动,当点N回到点C时,两个动点同时停止运动.⊙M是以M为圆心,1cm为半径的圆,设运动时间为t(s) (t>0)
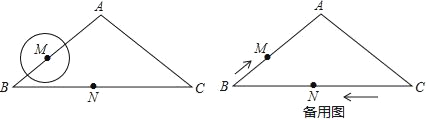
(1)tanB= ;
(2)当点M在线段AB上运动,且⊙M与BC相切时,求t的值;
(3)当t为何值时,⊙M与折线B﹣A﹣C的两个交点在等腰三角形ABC对称轴的同侧,且经过交点和点N的直线与⊙M相切?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com