
【题目】如图,点A(1,4)、B(2,a)在函数y=![]() (x>0)的图象上,直线AB与x轴相交于点C,AD⊥x轴于点D.
(x>0)的图象上,直线AB与x轴相交于点C,AD⊥x轴于点D.
(1)m= ;
(2)求点C的坐标;
(3)在x轴上是否存在点E,使以A、B、E为顶点的三角形与△ACD相似?若存在,求出点E的坐标;若不存在,说明理由.
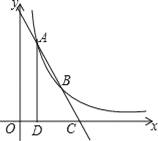
【答案】(1)4;(2)C的坐标为(3,0);(3)(﹣2,0).
【解析】试题分析:(1)把点代入求值.(2)先利用反比例函数求出A,B,点坐标,再利用待定系数法求直线方程.(3)假设存在E点,因为![]() ACD是直角三角形,假设
ACD是直角三角形,假设![]() ABE也是直角三角形,利用勾股定理分别计算A,B,C,是直角时AB长度,均与已知矛盾,所以不存在.
ABE也是直角三角形,利用勾股定理分别计算A,B,C,是直角时AB长度,均与已知矛盾,所以不存在.
试题解析:
解:(1)∵点A(1,4)在反比例函数y=![]() (x>0)的图象上,
(x>0)的图象上,
∴m=1×4=4,
故答案为:4.
(2)∵点B(2,a)在反比例函数y=![]() 的图象上,
的图象上,
∴a==2,
∴B(2,2).
设过点A、B的直线的解析式为y=kx+b,
∴![]() ,解得:
,解得:![]() ,
,
∴过点A、B的直线的解析式为y=﹣2x+6.
当y=0时,有﹣2x+6=0,
解得:x=3,
∴点C的坐标为(3,0).
(3)假设存在,设点E的坐标为(n,0).
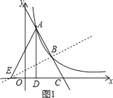
①当∠ABE=90°时(如图1所示),
∵A(1,4),B(2,2),C(3,0),
∴B是AC的中点,
∴EB垂直平分AC,EA=EC=n+3.
由勾股定理得:AD2+DE2=AE2,即42+(x+1)2=(x+3)2,
解得:x=﹣2,
此时点E的坐标为(﹣2,0);
②当∠BAE=90°时,∠ABE>∠ACD,
故△EBA与△ACD不可能相似;
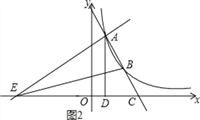
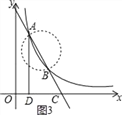
③当∠AEB=90°时,∵A(1,4),B(2,2),
∴AB=![]() ,2>
,2>![]() ,
,
∴以AB为直径作圆与x轴无交点(如图3),
∴不存在∠AEB=90°.
综上可知:在x轴上存在点E,使以A、B、E为顶点的三角形与△ACD相似,点E的坐标为(﹣2,0).


科目:初中数学 来源: 题型:
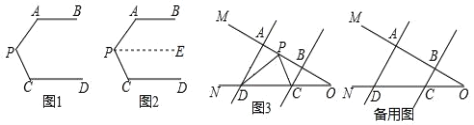
【题目】(1)如图1,AB∥CD,∠PAB=120°,∠PCD=110°,求∠APC的度数.小颖同学的解题思路是:如图2,过点P作PE∥AB,请你接着完成解答;如图3,点A、B在射线OM上,点C、D在射线ON上,AD∥BC,点P在射线OM上运动(点P与A、B、O三点不重合).
(2)当点P在线段AB上运动时,判断∠CPD与∠ADP、∠BCP之间的数量关系,并说明理由;
(3)当点P在线段AB外运动时,判断∠CPD与∠ADP、∠BCP之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,平行四边形ABCD的中心E的坐标为(2,0),若点A的坐标为(-2,1),则点C的坐标为( )
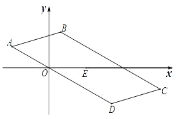
A. (4,-1)B. (6,-1)C. (8,-1)D. (6,-2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD中,AB=4,AD=2,点Q与点P同时从点A出发,点Q以每秒1个单位的速度沿A→D→C→B的方向运动,点P以每秒3个单位的速度沿A→B→C→D的方向运动,当P、Q两点相遇时,它们同时停止运动。设Q点运动的时间为![]() (秒),在整个运动过程中,求解下面问题:
(秒),在整个运动过程中,求解下面问题:
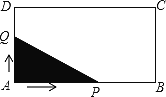
(1)当P、Q相遇时,求出![]() 的值(列方程解决问题);
的值(列方程解决问题);
(2)当△APQ的面积为![]() 时,此时t的值是_________;
时,此时t的值是_________;
(3)当△APQ为直角三角形时,直接写出相应的![]() 的值或取值范围.
的值或取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
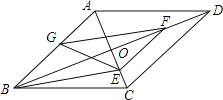
【题目】平行四边形ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD,AB的中点.下列结论:①EG=EF;②△EFG≌△GBE;③FB平分∠EFG;④EA平分∠GEF;⑤四边形BEFG是菱形.其中正确的是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
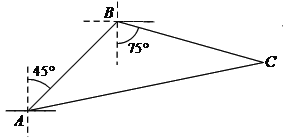
【题目】如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发,在C处成功拦截捕鱼船,求巡逻船从出发到成功拦截捕鱼船所用的时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com