
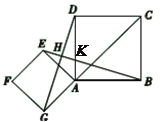
【题目】如图,点![]() 是正方形
是正方形![]() 对角线
对角线![]() 的延长线上任意一点,以线段
的延长线上任意一点,以线段![]() 为边作一个正方形
为边作一个正方形![]() ,线段
,线段![]() 和
和![]() 相交于点
相交于点![]() .
.
(1)求证:![]() ;
;
(2)判断![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
【答案】(1)证明见解析; (2)![]() ,理由见解析.
,理由见解析.
【解析】
(1)由四边形EFGA和四边形ABCD是正方形,易证得△GAD≌△EAB,即EB=GD;
(2)EB⊥GD,由(1)得∠ADG=∠ABE则在△DHK中,∠DHK=90°所以EB⊥GD;
(1)∵四边形ABCD是正方形
∴AB=AD, ∠DAB=90°
∵四边形AEFG是正方形
∴AE=AG, ∠EAG=90°
∴∠DAB=∠EAG
∴∠DAB+∠EAD=∠EAG+∠EAD
即∠BAE=∠DAG
∴![]()
∴![]()
(2)![]()
理由如下:
∵![]()
∴∠ABE=∠ADG
∵∠ABE+∠AKB=90°
∴ ∠ADG+∠AKB=90°
∵∠AKB=∠DKH
∴∠ADG+∠DKH=90°
∴∠DHK=90°
即![]() .
.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
【题目】如图1,将三角板放在正方形ABCD上,使三角板的直角顶点E与正方形ABCD的顶点A重合.三角板的一边交CD于点F,另一边交CB的延长线于点G.

(1)求证:EF=EG;
(2)如图2,移动三角板,使顶点E始终在正方形ABCD的对角线AC上,其他条件不变,(1)中的结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由;
(3)如图3,将(2)中的“正方形ABCD”改为“矩形ABCD”,且使三角板的一边经过点B,其他条件不变,若AB=a,BC=b,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
为了配合足球进校园的活动,实验学校在体育用品专卖店购买甲、乙两种不同的足球,购买甲种足球共花费2000元,购买乙种足球共花费1400元,购买甲种足球数量是购买乙种足球数量的2倍,且购买一个乙种足球比购买一个甲种足球多花20元。求购买一个甲种足球,一个乙种足球各需多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
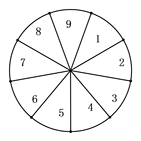
【题目】小亮和小芳都想参加学校杜团组织的暑假实践活动,但只有一个名额,小亮提议用如下的办法决定谁去等加活动:将一个转盘9等分,分别标上1至9九个号码,随意转动转盘,
若转到2的倍数,小亮去参加活动;转到3的倍数,小芳去参加活动;转到其它号码则重新特动转盘.
(1)转盘转到2的倍数的概率是多少?
(2)你认为这个游戏公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当三角形中一个内角是另一个内角的3倍时,我们称此三角形为“梦想三角形”.如果一个“梦想三角形”有一个角为108°,那么这个“梦想三角形”的最小内角的度数为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
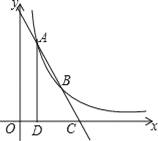
【题目】如图,点A(1,4)、B(2,a)在函数y=![]() (x>0)的图象上,直线AB与x轴相交于点C,AD⊥x轴于点D.
(x>0)的图象上,直线AB与x轴相交于点C,AD⊥x轴于点D.
(1)m= ;
(2)求点C的坐标;
(3)在x轴上是否存在点E,使以A、B、E为顶点的三角形与△ACD相似?若存在,求出点E的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a、b、c是![]() 的三边,且满足
的三边,且满足![]() ,试判断
,试判断![]() 的形状.
的形状.
阅读下面解题过程:
解:由![]() 得:
得:![]() ①
①
![]() ②
②
即![]() ③
③
∴![]() 为Rt△.④
为Rt△.④
试问:以上解题过程是否正确:_________.
若不正确,请指出错在哪步?______(填代号)
错误原因是______________________.
本题的结论应为_______________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】百货商店销售某种冰箱,每台进价2500元。市场调研表明:当销售价为2900元时,平均每天能售出8台;每台售价每降低10元时,平均每天能多售出1台。(销售利润=销售价—进价)
(1)如果设每台冰箱降价x元,那么每台冰箱的销售利润为 元,平均每天可销售冰箱 台;(用含x的代数式表示)
(2)商店想要使这种冰箱的销售利润平均每天达到5600元,且尽可能地清空冰箱库存,每台冰箱的定价应为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市出租车计费方法如图所示,![]() 表示行驶里程,
表示行驶里程,![]() (元)表示车费,请根据图象回答下列问题:
(元)表示车费,请根据图象回答下列问题:
(1)出租车的起步价是多少元;
(2)当 ![]() 时,求
时,求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)若某乘客有一次乘出租车的车费为32元,求这位乘客乘车的里程.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com