
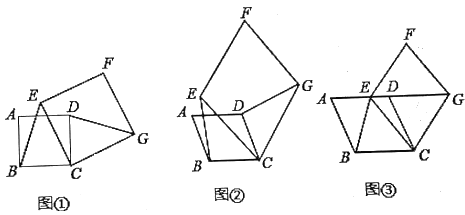
【题目】(1)(感知)如图①,四边形![]() 、
、![]() 均为正方形.
均为正方形.![]() 与
与![]() 的数量关系为________;
的数量关系为________;
(2)(拓展)如图②,四边形![]() 、
、![]() 均为菱形,且
均为菱形,且![]() .请判断
.请判断![]() 与
与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
(3)(应用)如图③,四边形![]() 、
、![]() 均为菱形,点
均为菱形,点![]() 在边
在边![]() 上,点
上,点![]() 在
在![]() 延长线上.若
延长线上.若![]() ,
,![]() ,
,![]() 的面积为9,则菱形
的面积为9,则菱形![]() 的面积为_______.
的面积为_______.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)24.
;(3)24.
【解析】
(1)根据正方形的性质证明△BCE≌△DCG即可求解;
(2)根据菱形的性质证明△BCE≌△DCG即可求解;
(3)由AD∥BC,△BCE≌△DCG可得S△ABE+S△CDE=S△BEC=S△CDG=9,又AE=2ED,可求出△CDE的面积,继而求出答案.
解:(1) ∵四边形![]() 、
、![]() 均为正方形
均为正方形
∴BC=DC,EC=GC,
∵![]()
即![]() .
.
∴![]()
∴![]()
(2)∵四边形![]() 、四边形
、四边形![]() 均为菱形,
均为菱形,
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]()
即![]() .
.
∴![]() ,
,
∴![]() .
.
(3)∵四边形ABCD为菱形,∴AD∥BC,
∴△BCE≌△DCG可得S△ABE+S△CDE=S△BEC=S△CDG=9,又AE=2ED,
∴S△CDE=![]()
∴S△ECG=S△CDE+S△CDG=12,
∴S菱形CEFG=2S△ECG=24.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某文具店用1050元购进第一批某种钢笔,很快卖完,又用1440元购进第二批该种钢笔,但第二批每支钢笔的进价是第一批进价的1.2倍,数量比第一批多了10支。
(1)求第一批每支钢笔的进价是多少元?
(2)第二批钢笔按24元/支的价格销售,销售一定数量后,根据市场情况,商店决定对剩余的钢笔全按8折一次性打折销售,但要求第二批钢笔的利润率不低于20%,问至少销售多少支后开始打折?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(材料阅读)数轴是数学学习的一个很重要的工具,利用数轴可以将数与形完美结合.通过数轴我们可发现许多重要的规律:
①对值的几何意义:一般地,若点![]() 、点
、点![]() 在数轴上表示的有理数分别为
在数轴上表示的有理数分别为![]() ,
,![]() ,那么
,那么![]() 、
、![]() 两点之间的距离表示为
两点之间的距离表示为![]() ,记作
,记作![]() ,
,![]() 则表示数
则表示数![]() 和1在数轴上对应的两点之间的距离;又如
和1在数轴上对应的两点之间的距离;又如![]() ,所以
,所以![]() 表示数
表示数![]() 和
和![]() 在数轴上对应的两点之间的距离;
在数轴上对应的两点之间的距离;
②若数轴上点![]() 、点
、点![]() 表示的数分别为
表示的数分别为![]() 、
、![]() ,那么线段
,那么线段![]() 的中点
的中点![]() 表示的数为
表示的数为![]() .
.
(问题情境)如图,在数轴上,点![]() 表示的数为
表示的数为![]() ,点
,点![]() 在原点右侧,表示的数为
在原点右侧,表示的数为![]() ,动点
,动点![]() 从点
从点![]() 出发以每秒
出发以每秒![]() 个单位长度的速度沿数轴正方向运动,同时,动点
个单位长度的速度沿数轴正方向运动,同时,动点![]() 从点
从点![]() 出发以每秒
出发以每秒![]() 个单位长度的速度沿数轴负方向运动,其中线段
个单位长度的速度沿数轴负方向运动,其中线段![]() 的中点记作点
的中点记作点![]() .
.
![]()
(综合运用)
(1)出发![]() 秒后,点
秒后,点![]() 和点
和点![]() 相遇,则
相遇,则![]() 表示的数
表示的数![]() ___________;
___________;
(2)在第(1)问的基础上,当![]() 时,求运动时间;
时,求运动时间;
(3)在第(1)问的基础上,点![]() 、
、![]() 在相遇后继续以原来的速度在这条数轴上运动,但
在相遇后继续以原来的速度在这条数轴上运动,但![]() 、
、![]() 两点运动的方向相同.随着点
两点运动的方向相同.随着点![]() 、
、![]() 的运动,线段
的运动,线段![]() 的中点
的中点![]() 也相应移动,问线段
也相应移动,问线段![]() 的中点
的中点![]() 能否与表示
能否与表示![]() 的点重合?若能,求出从
的点重合?若能,求出从![]() 、
、![]() 相遇起经过的运动时间;若不能,请说明理由.
相遇起经过的运动时间;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
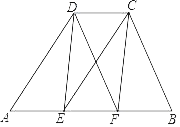
【题目】已知:如图,在四边形ABCD中,AB=3CD,AB∥CD,CE∥DA,DF∥CB.
(1)求证:四边形CDEF是平行四边形;
(2)填空:
①当四边形ABCD满足条件 时(仅需一个条件),四边形CDEF是矩形;
②当四边形ABCD满足条件 时(仅需一个条件),四边形CDEF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
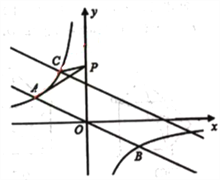
【题目】如图,直角坐标系中,直线![]() 与反比例函数
与反比例函数![]() 的图象交于A,B两点,已知A点的纵坐标是2.
的图象交于A,B两点,已知A点的纵坐标是2.
(1)求反比例函数的解析式.
(2)将直线![]() 沿x轴向右平移6个单位后,与反比例函数在第二象限内交于点C.动点P在y轴正半轴上运动,当线段PA与线段PC之差达到最大时,求点P的坐标.
沿x轴向右平移6个单位后,与反比例函数在第二象限内交于点C.动点P在y轴正半轴上运动,当线段PA与线段PC之差达到最大时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
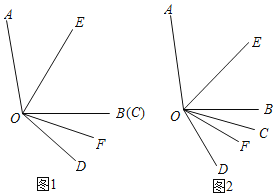
【题目】已知∠AOB=110°,∠COD=40°,OE平分∠AOC,OF平分∠BOD.
(1)如图1,当OB、OC重合时,求∠AOE﹣∠BOF的值;
(2)如图2,当∠COD从图1所示位置绕点O以每秒3°的速度顺时针旋转t秒(0<t<10),在旋转过程中∠AOE﹣∠BOF的值是否会因t的变化而变化?若不发生变化,请求出该定值;若发生变化,请说明理由.
(3)在(2)的条件下,当∠COF=14°时,t= 秒.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,正比例函数y=x的图象与一次函数y=kx﹣k的图象的交点坐标为A(m,2).
(1)求m的值和一次函数的解析式;
(2)设一次函数y=kx﹣k的图象与y轴交于点B,求△AOB的面积;
(3)直接写出使函数y=kx﹣k的值大于函数y=x的值的自变量x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
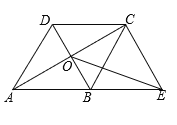
【题目】在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE∥DB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若∠DAB=60°,且AB=4,求OE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com