
【题目】(材料阅读)数轴是数学学习的一个很重要的工具,利用数轴可以将数与形完美结合.通过数轴我们可发现许多重要的规律:
①对值的几何意义:一般地,若点![]() 、点
、点![]() 在数轴上表示的有理数分别为
在数轴上表示的有理数分别为![]() ,
,![]() ,那么
,那么![]() 、
、![]() 两点之间的距离表示为
两点之间的距离表示为![]() ,记作
,记作![]() ,
,![]() 则表示数
则表示数![]() 和1在数轴上对应的两点之间的距离;又如
和1在数轴上对应的两点之间的距离;又如![]() ,所以
,所以![]() 表示数
表示数![]() 和
和![]() 在数轴上对应的两点之间的距离;
在数轴上对应的两点之间的距离;
②若数轴上点![]() 、点
、点![]() 表示的数分别为
表示的数分别为![]() 、
、![]() ,那么线段
,那么线段![]() 的中点
的中点![]() 表示的数为
表示的数为![]() .
.
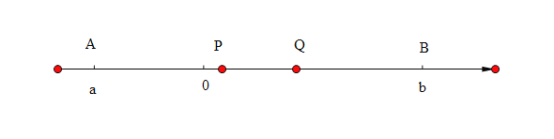
(问题情境)如图,在数轴上,点![]() 表示的数为
表示的数为![]() ,点
,点![]() 在原点右侧,表示的数为
在原点右侧,表示的数为![]() ,动点
,动点![]() 从点
从点![]() 出发以每秒
出发以每秒![]() 个单位长度的速度沿数轴正方向运动,同时,动点
个单位长度的速度沿数轴正方向运动,同时,动点![]() 从点
从点![]() 出发以每秒
出发以每秒![]() 个单位长度的速度沿数轴负方向运动,其中线段
个单位长度的速度沿数轴负方向运动,其中线段![]() 的中点记作点
的中点记作点![]() .
.
![]()
(综合运用)
(1)出发![]() 秒后,点
秒后,点![]() 和点
和点![]() 相遇,则
相遇,则![]() 表示的数
表示的数![]() ___________;
___________;
(2)在第(1)问的基础上,当![]() 时,求运动时间;
时,求运动时间;
(3)在第(1)问的基础上,点![]() 、
、![]() 在相遇后继续以原来的速度在这条数轴上运动,但
在相遇后继续以原来的速度在这条数轴上运动,但![]() 、
、![]() 两点运动的方向相同.随着点
两点运动的方向相同.随着点![]() 、
、![]() 的运动,线段
的运动,线段![]() 的中点
的中点![]() 也相应移动,问线段
也相应移动,问线段![]() 的中点
的中点![]() 能否与表示
能否与表示![]() 的点重合?若能,求出从
的点重合?若能,求出从![]() 、
、![]() 相遇起经过的运动时间;若不能,请说明理由.
相遇起经过的运动时间;若不能,请说明理由.
【答案】(1)![]() ;
;
(2)8秒或者16秒;
(3)![]() 能与表示
能与表示![]() 的点重合,
的点重合,![]() 秒.
秒.
【解析】
(1)根据题意即可得到结论;
(2)由(1)可知点![]() 和点
和点![]() 在点A与B上运动时相遇的时间是12秒,求出
在点A与B上运动时相遇的时间是12秒,求出![]() 、
、![]() 两点在
两点在![]() 上运动,相遇的时间
上运动,相遇的时间![]() ,则可以利用两个相遇时间的差,得出没相遇时,满足
,则可以利用两个相遇时间的差,得出没相遇时,满足![]() 的时间,或者利用两个相遇时间的和,得出相遇后,点
的时间,或者利用两个相遇时间的和,得出相遇后,点![]() 和点
和点![]() 继续运动,满足
继续运动,满足![]() 时的时间;
时的时间;
(3)当线段![]() 的中点
的中点![]() 与表示
与表示![]() 的点重合时,点
的点重合时,点![]() 和点
和点![]() 向数轴的负方向运动,设点
向数轴的负方向运动,设点![]() 表示的数是x,点
表示的数是x,点![]() 表示的数是y,由此可得
表示的数是y,由此可得![]() ,并根据中点的数的表示公式
,并根据中点的数的表示公式![]() ,化简求值即可.
,化简求值即可.
解:(1)依题意得:![]() ,并且
,并且![]() ,
,
则有![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
(2)
如图示:
∵![]()
∴设![]() 、
、![]() 两点在
两点在![]() 上运动,相遇的时间是
上运动,相遇的时间是![]() ,则,
,则,
依题意得:![]() ,
,
解之得:![]() ,
,
由(1)可知,在![]() 上出发
上出发![]() 秒后,点
秒后,点![]() 和点
和点![]() 相遇,
相遇,
∴当点![]() 和点
和点![]() 没相遇时,使
没相遇时,使![]() ,
,
时间为:![]() ,
,
当点![]() 和点
和点![]() 相遇又分开时,使
相遇又分开时,使![]() ,
,
时间为:![]() ,
,
即:出发8秒或者16秒后,![]() ,
,
(3)![]() 能与表示
能与表示![]() 的点重合,
的点重合,
线段![]() 的中点
的中点![]() 与表示
与表示![]() 的点重合时,点
的点重合时,点![]() 和点
和点![]() 向数轴的负方向运动,
向数轴的负方向运动,
如图示:

点![]() 和点
和点![]() 在C点相遇,
在C点相遇,
∴![]() ,
,
∴点C 表示的数是4,
设点![]() 表示的数是x,点
表示的数是x,点![]() 表示的数是y,
表示的数是y,
则依题意得:![]() ,
,
化简得:![]() ,
,
并且,根据中点的数的表示公式可得:![]() ,
,
即有:![]() ,代入
,代入![]() ,
,
则可得:![]() ,
,
∴![]() ,
,
∴当线段![]() 的中点
的中点![]() 是表示
是表示![]() 的点时,从
的点时,从![]() 、
、![]() 相遇起经过的运动时间为:
相遇起经过的运动时间为:![]() (秒),
(秒),


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
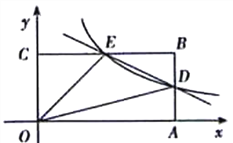
【题目】如图,在平面直角坐标系中,原点O是矩形OABC的一个顶点,点A、C都
在坐标轴上,点B的坐标是(4.2),反比例函数![]() 与AB,BC分别交于点D,E。
与AB,BC分别交于点D,E。
(1)求直线DE的解析式;
(2)若点F为y轴上一点,△OEF和△ODE的面积相等,求点F的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个由5张纸片拼成的平行四边形,相邻纸片之间互不重叠也无缝隙,其中两张等腰直角三角形纸片的面积都为S1,另两张直角三角形纸片的面积都为S2,中间一张正方形纸片的面积为S3,则这个平行四边形的面积可以表示为( )
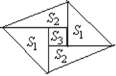
A. 4S1B. 4S2C. 4S2+S3D. 2S1+8S3
查看答案和解析>>
科目:初中数学 来源: 题型:
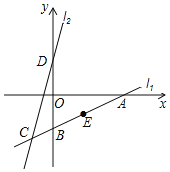
【题目】如图,直线l1:y=![]() x-4分别与x轴,y轴交于A,B两点,与直线l2交于点C(-2,m).点D是直线l2与y轴的交点,将点A向上平移3个单位,再向左平移8个单位恰好能与点D重合.
x-4分别与x轴,y轴交于A,B两点,与直线l2交于点C(-2,m).点D是直线l2与y轴的交点,将点A向上平移3个单位,再向左平移8个单位恰好能与点D重合.
(1)求直线l2的解析式;
(2)已知点E(n,-2)是直线l1上一点,将直线l2沿x轴向右平移.在平移过程中,当直线l2与线段BE有交点时,求平移距离d的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径作⊙O分别交AC,BM于点D,E.
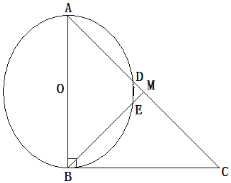
(1)求证:MD=ME
(2)填空:①若AB=6,当AD=2DM时,DE=___________;
②连接OD,OE,当∠A的度数为____________时,四边形ODME是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游泳馆普通票价20元/张,暑假为了促销,新推出两种优惠卡:
①金卡售价600元/张,每次凭卡不再收费.
②银卡售价150元/张,每次凭卡另收10元.
暑假普通票正常出售,两种优惠卡仅限暑假使用,不限次数.设游泳x次时,所需总费用为y元.

(1)分别写出选择银卡、普通票消费时,y与x之间的函数关系式;
(2)在同一坐标系中,若三种消费方式对应的函数图象如图所示,请求出点A、B、C的坐标;
(3)请根据函数图象,直接写出选择哪种消费方式更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
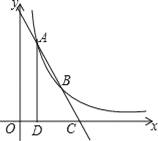
【题目】如图,点A(1,4)、B(2,a)在函数y=![]() (x>0)的图象上,直线AB与x轴相交于点C,AD⊥x轴于点D.
(x>0)的图象上,直线AB与x轴相交于点C,AD⊥x轴于点D.
(1)m= ;
(2)求点C的坐标;
(3)在x轴上是否存在点E,使以A、B、E为顶点的三角形与△ACD相似?若存在,求出点E的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
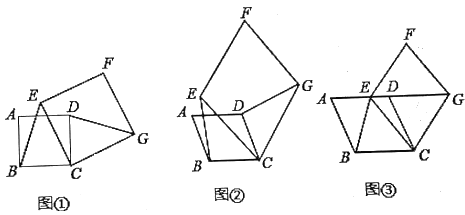
【题目】(1)(感知)如图①,四边形![]() 、
、![]() 均为正方形.
均为正方形.![]() 与
与![]() 的数量关系为________;
的数量关系为________;
(2)(拓展)如图②,四边形![]() 、
、![]() 均为菱形,且
均为菱形,且![]() .请判断
.请判断![]() 与
与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
(3)(应用)如图③,四边形![]() 、
、![]() 均为菱形,点
均为菱形,点![]() 在边
在边![]() 上,点
上,点![]() 在
在![]() 延长线上.若
延长线上.若![]() ,
,![]() ,
,![]() 的面积为9,则菱形
的面积为9,则菱形![]() 的面积为_______.
的面积为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,已知直线y=﹣![]() x+8与x轴、y轴分别交于A、B两点.直线OD⊥直线AB于点D.现有一点P从点D出发,沿线段DO向点O运动,另一点Q从点O出发,沿线段OA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到O时,两点都停止.设运动时间为t秒.
x+8与x轴、y轴分别交于A、B两点.直线OD⊥直线AB于点D.现有一点P从点D出发,沿线段DO向点O运动,另一点Q从点O出发,沿线段OA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到O时,两点都停止.设运动时间为t秒.
(1)点A的坐标为_____;线段OD的长为_____.
(2)设△OPQ的面积为S,求S与t之间的函数关系(不要求写出取值范围),并确定t为何值时S的值最大?
(3)是否存在某一时刻t,使得△OPQ为等腰三角形?若存在,写出所有满足条件的t的值;若不存在,则说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com