
����Ŀ����֪��AOB��110�㣬��COD��40�㣬OEƽ�֡�AOC��OFƽ�֡�BOD��
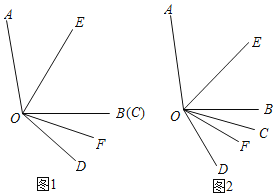
��1����ͼ1����OB��OC�غ�ʱ�����AOE����BOF��ֵ��
��2����ͼ2������COD��ͼ1��ʾλ���Ƶ�O��ÿ��3����ٶ�˳ʱ����תt�루0��t��10��������ת�����С�AOE����BOF��ֵ�Ƿ����t�ı仯���仯�����������仯��������ö�ֵ���������仯����˵�����ɣ�
��3���ڣ�2���������£�����COF��14��ʱ��t���� ���룮
���𰸡���1��35�㣻��2����AOE����BOF��ֵ�Ƕ�ֵ�����������������3��![]() ��
��
��������
��1�����ȸ��ݽ�ƽ���ߵĶ�����á�AOE�͡�BOF�Ķ�����Ȼ����ݡ�AOE����BOF��⣻
��2������������á�BOC��3t�����ٸ��ݽ�ƽ���ߵĶ���á�AOC����AOB+3t������BOD����COD+3t����Ȼ���ɽ�ƽ���ߵĶ����ɣ�
��3����������á�BOF����3t+14��������![]() ���ⷽ�̼������t��ֵ��
���ⷽ�̼������t��ֵ��
�⣺��1����OEƽ�֡�AOC��OFƽ�֡�BOD��
��![]() ��55����
��55����![]() ��
��
���AOE����BOF��55����20����35����
��2����AOE����BOF��ֵ�Ƕ�ֵ
�������BOC��3t����
���AOC����AOB+3t����110��+3t������BOD����COD+3t����40��+3t����
��OEƽ�֡�AOC��OFƽ�֡�BOD��
![]()
![]()
��![]() ��
��
��![]() ��
��
���AOE����BOF��ֵ�Ƕ�ֵ����ֵΪ35����
��3����������á�BOF����3t+14������
��![]() ��
��
���![]() ��
��
�ʴ�Ϊ![]() ��
��


 ��һ������Ԫͬ�����ؾ�ϵ�д�
��һ������Ԫͬ�����ؾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ����5��ֽƬƴ�ɵ�ƽ���ı��Σ�����ֽƬ֮�以���ص�Ҳ��϶���������ŵ���ֱ��������ֽƬ�������ΪS1��������ֱ��������ֽƬ�������ΪS2���м�һ��������ֽƬ�����ΪS3�������ƽ���ı��ε�������Ա�ʾΪ�� ��
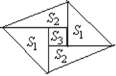
A. 4S1B. 4S2C. 4S2��S3D. 2S1��8S3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
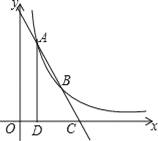
����Ŀ����ͼ����A��1��4����B��2��a���ں���y=![]() ��x��0����ͼ���ϣ�ֱ��AB��x���ཻ�ڵ�C��AD��x���ڵ�D��
��x��0����ͼ���ϣ�ֱ��AB��x���ཻ�ڵ�C��AD��x���ڵ�D��
��1��m=������
��2�����C�����ꣻ
��3����x�����Ƿ���ڵ�E��ʹ��A��B��EΪ���������������ACD���ƣ������ڣ������E�����ꣻ�������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
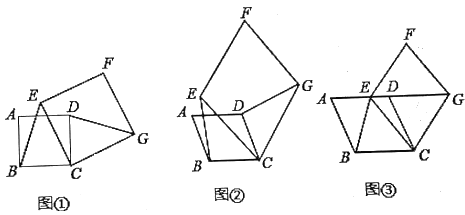
����Ŀ��(1)����֪����ͼ�٣��ı���![]() ��
��![]() ��������.
��������.![]() ��
��![]() ��������ϵΪ________��
��������ϵΪ________��
(2)����չ����ͼ�ڣ��ı���![]() ��
��![]() ��������
��Ϊ���Σ���![]() .���ж�
.���ж�![]() ��
��![]() ��������ϵ����˵�����ɣ�
��������ϵ����˵�����ɣ�
(3)��Ӧ�ã���ͼ�ۣ��ı���![]() ��
��![]() ��������
��Ϊ���Σ���![]() �ڱ�
�ڱ�![]() �ϣ���
�ϣ���![]() ��
��![]() �ӳ�����.��
�ӳ�����.��![]() ��
��![]() ��
��![]() �����Ϊ9��������
�����Ϊ9��������![]() �����Ϊ_______.
�����Ϊ_______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y����![]() x+
x+![]() ��x�ᡢy��ֱ��ڵ�A��B�������������ҵ�P��ʹ��ABPΪ���������Σ����P�ĸ���Ϊ�� ��
��x�ᡢy��ֱ��ڵ�A��B�������������ҵ�P��ʹ��ABPΪ���������Σ����P�ĸ���Ϊ�� ��

A. 2B. 4C. 6D. 8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������ϵ�A1��A2��A3��A4������A20����20��������ʾ�����ֱ���a1��a2��a3��a4������a20����A1A2��A2A3��������A19A20����a3��20��|a1��a4|��12��
![]()
��1���߶�A3A4�ij��ȣ��� ����a2���� ����
��2����|a1��x|��a2+a4����x��ֵ��
��3���߶�MN��O����������˶������߶�MN���߶�A1A20��ʼ���ص����ֵ���ȫû���ص����־�����9�룮���߶�MN��5�����߶�MN���˶��ٶȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������мӴ���ְ����Ͷ��������ȡ�������õ����Ч����ijУ��������˾��꼶m��ѧ������ѧ�����������ݵ��������Ƴ�����������������ͳ��ͼ���������ͼ�е���Ϣ�������������

��1��m=______ ��
��2������ͳ��ͼ����ְ������Ӧ�����ε�Բ�Ľ���=______ ��
��3���벹ȫ����ͳ��ͼ��
��4������У���꼶��ѧ��900�������Ƹ�У���ж�������ҵ������ѧ������ְ�ߣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬��ֱ֪��y=��![]() x+8��x�ᡢy��ֱ���A��B���㣮ֱ��OD��ֱ��AB�ڵ�D������һ��P�ӵ�D���������߶�DO���O�˶�����һ��Q�ӵ�O���������߶�OA���A�˶�������ͬʱ�������ٶȶ�Ϊÿ��1����λ���ȣ�����P�˶���Oʱ�����㶼ֹͣ�����˶�ʱ��Ϊt�룮
x+8��x�ᡢy��ֱ���A��B���㣮ֱ��OD��ֱ��AB�ڵ�D������һ��P�ӵ�D���������߶�DO���O�˶�����һ��Q�ӵ�O���������߶�OA���A�˶�������ͬʱ�������ٶȶ�Ϊÿ��1����λ���ȣ�����P�˶���Oʱ�����㶼ֹͣ�����˶�ʱ��Ϊt�룮
��1����A������Ϊ_____���߶�OD�ij�Ϊ_____��
��2������OPQ�����ΪS����S��t֮��ĺ�����ϵ����Ҫ��д��ȡֵ��Χ������ȷ��tΪ��ֵʱS��ֵ���
��3���Ƿ����ijһʱ��t��ʹ����OPQΪ���������Σ������ڣ�д����������������t��ֵ���������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� �۲�����������ʽ��2+2��2��2��3+![]() ��3��
��3��![]() �������������£����dz�ʹ��ʽa+b��ab������һ��������a��bΪ����Ȥ���ԡ�����Ϊ��a��b���磺���ԣ�2��2������3��
�������������£����dz�ʹ��ʽa+b��ab������һ��������a��bΪ����Ȥ���ԡ�����Ϊ��a��b���磺���ԣ�2��2������3��![]() �����ǡ���Ȥ���ԡ���
�����ǡ���Ȥ���ԡ���
��1�����ԣ�0��0������5��![]() �����ǡ���Ȥ���ԡ������� ����
�����ǡ���Ȥ���ԡ������� ����
��2������a��![]() ���ǡ���Ȥ���ԡ�����a��ֵ��
���ǡ���Ȥ���ԡ�����a��ֵ��
��3������д��һ�Է��������ġ���Ȥ���ԡ��� ����
��ע�⣺��������Ŀ�����еġ���Ȥ���ԡ��ظ���
��4������a2+a��4���ǡ���Ȥ���ԡ���3��2a2��2a��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com