
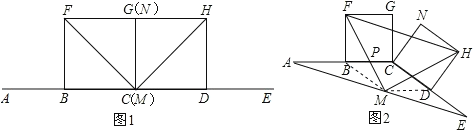
【题目】在图1、图2中,线段AC=CE,点B是线段AC的中点,点D是线段CE的中点,四边形BCGF和CDHN都是正方形,AE的中点是M.如图1,点E在AC的延长线上,点N与点G重合时,点M与点C重合,容易证明FM=MH,FM⊥HM;现将图1的CE绕点C顺时针旋转一个锐角,得到图2,判断△FMH的形状,并证明你的结论.

【答案】△FMH是等腰直角三角形,理由见解析
【解析】分析:连接BM,MD,MF交AC于P,根据三角形中位线定理求出MD∥BC,![]() MB∥CD,
MB∥CD,![]() 得出平行四边形
得出平行四边形![]() ,求出∠CBM=∠CDM,根据SAS证△FBM≌△HDM,推出FM=MH,∠FMB=∠MHD,∠BFM=∠DHM,即可求出
,求出∠CBM=∠CDM,根据SAS证△FBM≌△HDM,推出FM=MH,∠FMB=∠MHD,∠BFM=∠DHM,即可求出![]() 即可得出答案.
即可得出答案.
详解:△FMH是等腰直角三角形,
证明:连接BM,MD,MF交AC于P,
∵B、D.M分别是AC、CE、AE的中点,
∴MD∥BC,![]()
MB∥CD,![]()
∴四边形BCDM是平行四边形,
∴∠CBM=∠CDM,
∵![]()
∴∠FBM=∠MDH,
∵FB=HD,BM=DM,
∴△FBM≌△HDM,
∴FM=MH,∠FMB=∠MHD,∠BFM=∠DHM,
∴![]()
∴△FMH是等腰直角三角形.


科目:初中数学 来源: 题型:
【题目】油箱中有油30kg,油从管道中匀速流出,1小时流完,求油箱中剩余油量Q(kg)与流出时间t(分钟)间的函数关系式为__________________,自变量的范围是_____________.当Q=10kg时,t=_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,图2,分别是吊车在吊一物品时的实物图与示意图,已知吊车底盘CD的高度为1.8米,支架BC的长为4米,且与地面成30°角,吊绳AB与支架BC的夹角为80°,吊臂AC与地面成70°角,求吊车的吊臂顶端A点距地面的高度是多少米?(精确到0.1米,参考数据:sin10°=cos80°=0.17,cos10°=sin80°=0.98,sin20°=cos70°=0.34,tan70°=2.75,sin70°=0.94)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是△ABC的内心,BO的延长线和△ABC的外接圆相交于D,连结DC、DA、OA、OC,四边形OADC为平行四边形.
(1)求证:△BOC≌△CDA.
(2)若AB=2,求阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
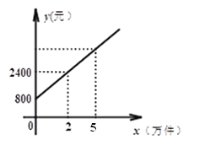
【题目】某公司市场营销部的某营销员的个人月收入与该营销员每月的销售量成一次函数关系,其图像如图所示.根据图像提供的信息,解答下列问题:
(1)求营销员的个人月收入y元与该营销员每月的销售量x万件(x≥0)之间的函数关系式;
(2)若两个月内该营销员的销售量从2万件猛增到5万件,月收入两个月大幅度增长,且连续两个月的月收入的增长率是相同的,试求这个增长率(![]() ,保留到百分位).
,保留到百分位).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条不完整的数轴上从左到右有点A,B,D,C,其中AB=2,BD=3,DC=1,如图所示,设点A,B,D,C所对应数的和是p.
(1)①若以B为原点.写出点A,D,C所对应的数,并计算p的值;
②若以D为原点,p又是多少?
(2)若原点O在图中数轴上点C的右边,且CO=x,p=﹣71,求x.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市交警大队一辆警车每天在一段东西方向的公路上巡逻执法.一天上午从![]() 地出发,中午到达
地出发,中午到达![]() 地,规定向东行驶的里程为正,向西行驶的里程为负,这天行驶的里程数记录如下(单位:
地,规定向东行驶的里程为正,向西行驶的里程为负,这天行驶的里程数记录如下(单位:![]() );
);![]() ,
,
(1)问![]() 地在
地在![]() 地的东面还是西面?
地的东面还是西面?![]() ,
,![]() 两地相距多少千米?
两地相距多少千米?
(2)若该警车每千米耗油![]() 升,警车出发时,油箱中有油
升,警车出发时,油箱中有油![]() 升,请问中途有没有给警车加过油?若有,至少加了多少升油?请说明理由.
升,请问中途有没有给警车加过油?若有,至少加了多少升油?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
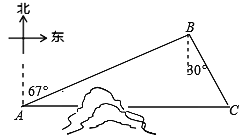
【题目】如图,C地在A地的正东方向,因有大山阻隔,由A地到C地需绕行B地,现计划开凿隧道使A、C两地直线贯通,经测量得:B地在A地的北偏东67°方向,距离A地280km,C地在B地南偏东的30°方向.
(1)求B地到直线AC的距离;
(2)求隧道开通后与隧道开通前相比,从A地到C地的路程将缩短多少?
(本题结果都精确到0.1km)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高产品的附加值,某公司计划将研发生产的1200件新产品进行精加工后再投放市场.现有甲、乙两个工厂都具备加工能力,公司派出相关人员分别到这两个工厂了解情况,获得如下信息:
信息一:甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天;
信息二:乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍.
根据以上信息,求甲、乙两个工厂每天分别能加工多少件新产品.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com