
【题目】旅游公司在景区内配置了50辆观光车供游客租赁使用,假定每辆观光车一天内最多只能出租一次,且每辆车的日租金是x(元).发现每天的营运规律如下:当x不超过100元时,观光车能全部租出;当x超过100元时,每辆车的日租金每增加5元,租出去的观光车就会减少1辆.已知所有观光车每天的管理费是1100元.当每辆车的日租金为多少元时,每天的净收入最多?(注:净收入=租车收入管理费)
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】阅读下面的材料
勾股定理神秘而美妙,它的证法多种多样,下面是教材中介绍的一种拼图证明勾股定理的方法.
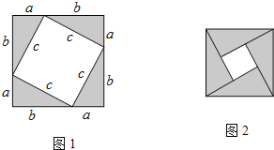
先做四个全等的直角三角形,设它们的两条直角边分别为a,b,斜边为c,然后按图1的方法将它们摆成正方形.
由图1可以得到![]() ,
,
整理,得![]() .
.
所以![]() .
.
(1)如果把图1中的四个全等的直角三角形摆成图2所示的正方形,
请你参照上述证明勾股定理的方法,用图2证明勾股定理.
(2)图2中若大正方形的面积是13,小正方形的面积是1,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)6-(+3)-(-7)+(-2);
(2)(-![]() -
-![]() +
+![]() )×(-36)
)×(-36)
(3) (﹣2)2+3×(﹣1)2016﹣(﹣4)×2 .
(4)6x2y-(-2x2y)
(5)(3a-2) -2(a-1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车和一辆摩托车分别从A,B两地去同一个城市,它们离A地的路程随时间变化的图象如图所示.则下列结论:①摩托车比汽车晚到1h;②A,B两地的路程为20km;③摩托车的速度为45km/h,汽车的速度为60km/h;④汽车出发1小时后与摩托车相遇,此时距B地40千米.其中正确结论的个数是( )
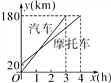
A. 2个 B. 3个 C. 4个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y﹣3与x成正比例,且x=2时,y=7.
(1)求出y与x之间的函数关系;
(2)画出函数的图象;
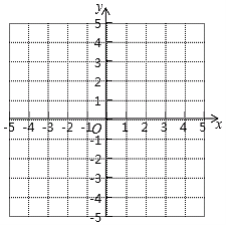
(3)结合所画出的图象直接写出当x满足什么条件时,函数的图象都在x轴的上方?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为确保信息安全,信息需加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密).安全员是数学爱好者,制定加密规则为:明文x,y,z对应密文x+y+z,x-y+z,x-y-z.例如:明文1,2,3对应密文6,2,-4.当接收方收到密文12,4,-6时,则解密得到的明文为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读以下两则材料,解决后续问题:
材料一:我们可以将任意三位数记为![]() (其中a,b,c,分别表示该数的百位数字、十位数字和个位数字,且a≠0,显然
(其中a,b,c,分别表示该数的百位数字、十位数字和个位数字,且a≠0,显然![]() =100a+10b+c.
=100a+10b+c.
材料二:若一个三位数的三个数字均不为0且三个数字互不相等,则称之为原始数,比如123就是一个原始数.将原始数的三个数位数字交换顺序,可产生出5个新的原始数,比如由123可以产生出132、213、231、312、321这5个新原始数.将这6个数相加,得到的和1332称为由原始数123生成的终止数.
问题:(1)求原始数247生成的终止数;
(2)试说明所有的原始数生成的终止数都能被222整除;
(3)若一个原始数生成的终止数为![]() ,求满足条件的所有原始数.
,求满足条件的所有原始数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在正方形ABCD中,E是AB上一点,G是AD上一点,∠ECG=45°,求证EG=BE+GD.

(2)请用(1)的经验和知识完成此题:如图2,在四边形ABCD中,AG//BC(BC>AG),∠B=90°,AB=BC=12,E是AB上一点,且∠ECG=45°,BE=4,求EG的长?
查看答案和解析>>
科目:初中数学 来源: 题型:
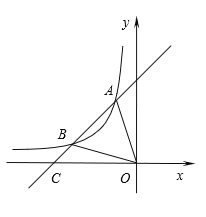
【题目】如图,一次函数y=x+4的图像与反比例函数![]() (k为常数且k≠0)的图像交于A(-1,a),B(b,1)两点,与x轴交于点C.
(k为常数且k≠0)的图像交于A(-1,a),B(b,1)两点,与x轴交于点C.
(1)求此反比例函数的表达式;
(2)若点P在x轴上,且![]() ,求点P的坐标.
,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com