
【题目】(题文)如图,某数学活动小组为测量学校旗杆AB的高度,从旗杆正前方2![]() m处的点C出发,沿斜面坡度i=1∶
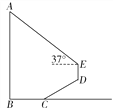
m处的点C出发,沿斜面坡度i=1∶![]() 的斜坡CD前进4m到达点D,在点D处安置测角仪,测得旗杆顶部A的仰角为37°,量得仪器的高DE为1.5 m.已知A,B,C,D,E在同一平面内,AB⊥BC,AB∥DE.求旗杆AB的高度.(参考数据:sin37°≈
的斜坡CD前进4m到达点D,在点D处安置测角仪,测得旗杆顶部A的仰角为37°,量得仪器的高DE为1.5 m.已知A,B,C,D,E在同一平面内,AB⊥BC,AB∥DE.求旗杆AB的高度.(参考数据:sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() ,计算结果保留根号)
,计算结果保留根号)
【答案】(3![]() +3.5)m.
+3.5)m.
【解析】试题延长ED交BC延长线于点F,则∠CFD=90°,Rt△CDF中求得CF、DF的长,作EG⊥AB,可得GE、GB的长,再求出AG的长,即可得答案.
试题解析:解:如图,延长ED交BC延长线于点F,则∠CFD=90°,∵tan∠DCF=i=![]() =
=![]() ,∴∠DCF=30°,∵CD=4,∴DF=
,∴∠DCF=30°,∵CD=4,∴DF=![]() CD=2,CF=CDcos∠DCF=4×
CD=2,CF=CDcos∠DCF=4×![]() =
=![]() ,∴BF=BC+CF=
,∴BF=BC+CF=![]() +
+![]() =
=![]() ,过点E作EG⊥AB于点G,则GE=BF=
,过点E作EG⊥AB于点G,则GE=BF=![]() ,GB=EF=ED+DF=1.5+2=3.5,又∵∠AED=37°,∴AG=GEtan∠AEG=
,GB=EF=ED+DF=1.5+2=3.5,又∵∠AED=37°,∴AG=GEtan∠AEG=![]() tan37°,则AB=AG+BG=
tan37°,则AB=AG+BG=![]() tan37°+3.5=
tan37°+3.5=![]() ,故旗杆AB的高度为(
,故旗杆AB的高度为(![]() )米.
)米.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
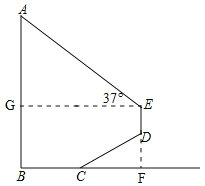
【题目】学完《平面直角坐标系》和《一次函数》这两章后,老师布置了这样一道思考题:已知:如图,在长方形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点,
的中点,![]() 和
和![]() 相交于点
相交于点![]() .求
.求![]() 的面积.小明同学应用所学知识,顺利地解决了此题,他的思路是这样的:以
的面积.小明同学应用所学知识,顺利地解决了此题,他的思路是这样的:以![]() 所在的直线为
所在的直线为![]() 轴,以
轴,以![]() 所在的直线为
所在的直线为![]() 轴建立适当的平面直角坐标系,写出图中一些点坐标.根据一次函数的知识求出点
轴建立适当的平面直角坐标系,写出图中一些点坐标.根据一次函数的知识求出点![]() 的坐标,从而求得
的坐标,从而求得![]() 的面积.请你按照小明的思路解决这道思考题.
的面积.请你按照小明的思路解决这道思考题.
查看答案和解析>>
科目:初中数学 来源: 题型:
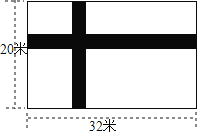
【题目】如图所示,宽为20米,长为32米的长方形地面上,修筑宽度为x米的两条互相垂直的小路,余下的部分作为耕地,如果要在耕地上铺上草皮,选用草皮的价格是每平米a元,
(1)求买草皮至少需要多少元?(用含a,x的式子表示)
(2)计算a=40,x=2时,草皮的费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个四位数,记千位上和百位上的数字之和为![]() ,十位上和个位上的数字之和为
,十位上和个位上的数字之和为![]() ,如果
,如果![]() ,那么称这个四位数为“和平数”.
,那么称这个四位数为“和平数”.
例如:1423,![]() ,
,![]() ,因为
,因为![]() ,所以1423是“和平数”.
,所以1423是“和平数”.
(1)直接写出:最小的“和平数”是 ,最大的“和平数”是 ;
(2)将一个“和平数”的个位上与十位上的数字交换位置,同时,将百位上与千位上的数字交换位置,称交换前后的这两个“和平数”为一组“相关和平数”.
例如:1423与4132为一组“相关和平数”
求证:任意的一组“相关和平数”之和是1111的倍数.
(3)求个位上的数字是千位上的数字的两倍且百位上的数字与十位上的数字之和是12的倍数的所有“和平数”;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,点C是直径AB延长线上一点,过点C作⊙O的切线,切点为D,连结BD.
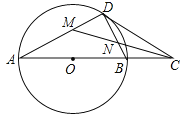
(1)求证:∠A=∠BDC;
(2)若CM平分∠ACD,且分别交AD、BD于点M、N,当DM=1时,求MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在⊙O中,AB= 4![]() ,AC是⊙O的直径,AC⊥BD于F,∠A=30°.
,AC是⊙O的直径,AC⊥BD于F,∠A=30°.

⑴求图中阴影部分的面积;
⑵若用阴影扇形OBD围成一个圆锥侧面,请求出这个圆锥底面圆的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题正确的有( )
①如果等腰三角形的底角为15°,那么腰上的高是腰长的一半;
②三角形至少有一个内角不大于60°;
③连结任意四边形各边中点形成的新四边形是平行四边形;
④十边形内角和为1800°.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个四边形的一条对角线把四边形分成两个等腰三角形,我们把这条对角线叫这个四边形的和谐线,这个四边形叫做和谐四边形.如菱形就是和谐四边形.

(1)如图1,在梯形ABCD中,AD∥BC,∠BAD=120°,∠C=75°,BD平分∠ABC.求证:BD是梯形ABCD的和谐线;
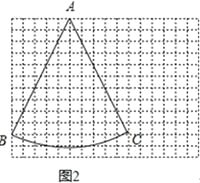
(2)如图2,在12×16的网格图上(每个小正方形的边长为1)有一个扇形BAC,点A.B.C均在格点上,请在答题卷给出的两个网格图上各找一个点D,使得以A、B、C、D为顶点的四边形的两条对角线都是和谐线,并画出相应的和谐四边形;
(3)四边形ABCD中,AB=AD=BC,∠BAD=90°,AC是四边形ABCD的和谐线,求∠BCD的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com