
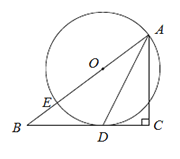
【题目】已知:如图,在Rt△ABC中,∠C=90°,点E在斜边AB上,以AE为直径的⊙O与BC边相切于点D,连结AD.
(1)求证:AD是∠BAC的平分线;
(2)若AC=3,BC=4,求⊙O的半径.
【答案】(1)证明见解析(2)![]()
【解析】试题分析:
(1)连接OD,由⊙O与BC边相切于点D可得∠ODB=∠C=90°,从而可得OD∥AC,由此即可得到∠CAD=∠ADO,由OD=OA可得∠DAO=∠ODA,即可得到∠CAD=∠DAO,从而得到AD是∠BAC的角平分线;
(2)在Rt△ABC中,由AC=3,BC=4易得AB=5,由tanB=![]() ,设OD=3x,则BD=4x,由此在Rt△OBD中可得OB=5x,结合OA=OD=3x可得AB=8x=5,解得x=
,设OD=3x,则BD=4x,由此在Rt△OBD中可得OB=5x,结合OA=OD=3x可得AB=8x=5,解得x=![]() ,即可得到⊙O的半径为:
,即可得到⊙O的半径为: ![]() .
.
试题分析:
(1)如图,连接OD,
∵⊙O与BC边相切于点D,
∴∠ODB=∠C=90°,
∴OD∥AC,
∴∠CAD=∠ADO,
∵OD=OA,
∴∠DAO=∠ODA,
∴∠CAD=∠DAO,
∴AD是∠BAC的角平分线;
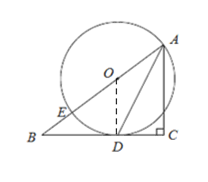
(2)∵在Rt△ABC中,由AC=3,BC=4,
∴AB=![]() ,
,
∵tanB=![]() ,
,
∴可设OD=3x,则BD=4x,
∴OB=![]() ,
,
又∵OA=OD=3x,
∴AB=3x+5x=8x=5,解得:x=![]() ,
,
∴⊙O的半径OD=3x=![]() .
.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx+b和反比例函数y=![]() 图象相交于A(2,4),B(n,﹣2)两点.
图象相交于A(2,4),B(n,﹣2)两点.
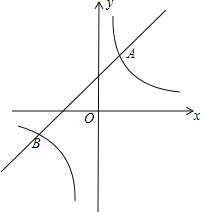
(1)求一次函数和反比例函数的解析式;
(2)观察图象,直接写出不等式kx+b﹣![]() <0的解集;
<0的解集;
(3)点C(a,b),D(a,c)(a>2)分别在一次函数和反比例函数图象上,且满足CD=2,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两校分别有一男一女共4名教师报名到农村中学支教.
(1)若从甲、乙两校报名的教师中分别随机选1名,则所选的2名教师性别相同的概率是 .
(2)若从报名的4名教师中随机选2名,用列表或画树状图的方法求出这2名教师来自同一所学校的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD分别与BC,OC相交于点E,F,则下列结论:
①AD⊥BD;②∠AOC=∠AEC;③CB平分∠ABD;④AF=DF;⑤BD=2OF;⑥△CEF≌△BED,其中一定成立的是( )
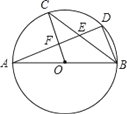
A. ②④⑤⑥ B. ①③⑤⑥ C. ②③④⑥ D. ①③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以40m/s的速度将小球沿与地面成30°角的方向击出时,小球的飞行路线是一条抛物线.如果不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系h=20t﹣5t2.
(1)小球飞行时间是多少时,小球最高?最大高度是多少?
(2)小球飞行时间t在什么范围时,飞行高度不低于15m?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着移动互联网的快速发展,基于互联网的共享单车应运而生.为了解某小区居民使用共享单车的情况,某研究小组随机采访该小区的10位居民,得到这10位居民一周内使用共享单车的次数分别为:17,12,15,20,17,0,7,26,17,9.
(1)这组数据的中位数是 ,众数是 ;
(2)计算这10位居民一周内使用共享单车的平均次数;
(3)若该小区有200名居民,试估计该小区居民一周内使用共享单车的总次数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABO中,AB⊥OB,OB=![]() ,AB=1,把△ABO绕点O旋转150°后得到△A1B1O,则点A1的坐标为
,AB=1,把△ABO绕点O旋转150°后得到△A1B1O,则点A1的坐标为

A.(﹣1,![]() ) B.(﹣1,
) B.(﹣1,![]() )或(﹣2,0) C.(
)或(﹣2,0) C.(![]() ,﹣1)或(0,﹣2) D.(
,﹣1)或(0,﹣2) D.(![]() ,﹣1)
,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
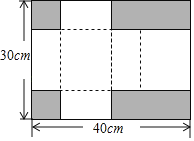
【题目】如图,将一张长方形纸板的四个角上分别剪掉2个小正方形和2个小长方形(阴影部分即剪掉的部分),剩余的部分可以折成一个有盖的长方体盒子(纸板的厚度忽略不计).若长方形纸板边长分别为40cm和30cm,且折成的长方体盒子表面积是950cm2,此时长方体盒子的体积为_____cm3.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com