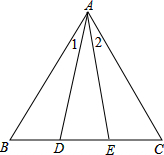
如图.B.D.E.C四点在同一条直线上.且AD=AE.∠1=∠2．求证:∠B=∠C．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

如图，B、D、E、C四点在同一条直线上，且AD=AE，∠1=∠2．求证：∠B=∠C（请不用三角形全等证明）．

考点：等腰三角形的性质

专题：证明题

分析：由AD=AE，可得∠ADE=∠AED，再利用外角的性质结合条件可证明∠B=∠C．

解答：证明：
∵AD=AE，
∴∠ADE=∠AED，
∴∠1+∠B=∠2+∠C，
∵∠1=∠2，
∴∠B=∠C．

点评：本题主要考查等腰三角形的性质，掌握等边对等角是解题的关键．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

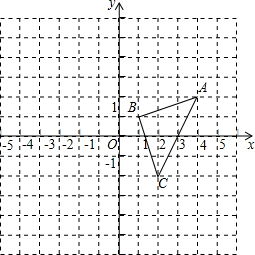如图，在平面直角坐标系中，已知△ABC的三个顶点A、B、C都在格点上，坐标分别为（4，2），（1，1），（2，-2）．
（1）将△ABC三个顶点的横坐标、纵坐标都分别乘-2，写出变化后的三个顶点A₁、B₁、C₁的坐标．
（2）画出以A₁、B₁、C₁为顶点的△A₁B₁C₁．
（3）△ABC与△A₁B₁C₁是位似图形吗？如果是位似图形，请指出位似中心和位似比．如果不是，请说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

解方程：

2(y-1)

y+2

-1．

查看答案和解析>>

科目：初中数学 来源： 题型：

某校为了美化校园，准备在一块长32米、宽20米的长方形场地上修筑若干条等宽道路，余下部分作草坪，并请全校同学参与设计，现在有两位学生各设计了一种方案（如图），根据两种设计方案各列出方程，求图中道路的宽分别是多少，使图（1）（2）的草坪面积为540平分米？