
【题目】阅读下列材料:
一般地,n个相同的因数a相乘![]() 记为an,记为an.如2×2×2=23=8,此时,3叫做以2为底8的对数,记为log28(即log28=3).一般地,若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为logab(即logab=n).如34=81,则4叫做以3为底81的对数,记为log381(即log381=4).
记为an,记为an.如2×2×2=23=8,此时,3叫做以2为底8的对数,记为log28(即log28=3).一般地,若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为logab(即logab=n).如34=81,则4叫做以3为底81的对数,记为log381(即log381=4).
(1)计算以下各对数的值:
log24= ,log216= ,log264= .
(2)观察(1)中三数4、16、64之间满足怎样的关系式,log24、log216、log264之间又满足怎样的关系式 。
(3)由(2)的结果,你能归纳出一个一般性的结论吗?
logaM+logaN= ;(a>0且a≠1,M>0,N>0)
(4)根据幂的运算法则:anam=an+m以及对数的含义证明上述结论.
【答案】(1)2,4,6;(2)4×16=64,log24+log216=log264;(3)loga(MN);(4)证明见解析.
【解析】试题分析:首先认真阅读题目,准确理解对数的定义,把握好对数与指数的关系.
(1)根据对数的定义求解;
(2)认真观察,不难找到规律:4×16=64,log24+log216=log264;
(3)有特殊到一般,得出结论:logaM+logaN=loga(MN);
(4)首先可设logaM=b1,logaN=b2,再根据幂的运算法则:anam=an+m以及对数的含义证明结论.
试题解析:(1)log24=2,log216=4,log264=6;
(2)4×16=64,log24+log216=log264;
(3)logaM+logaN=loga(MN);
(4)证明:设logaM=b1,logaN=b2,
则ab1=M,ab2=N,
∴MN=ab1ab2=ab1+b2,
∴b1+b2=loga(MN)即logaM+logaN=loga(MN).


科目:初中数学 来源: 题型:
【题目】如图,直线y=k1x+b与双曲线y=![]() 相交于点A(1,2),B(m,-1)两点.
相交于点A(1,2),B(m,-1)两点.
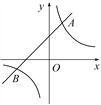
(1)分别求直线和双曲线的表达式;
(2)若A1(x1,y1),A2(x2,y2),A3(x3,y3)为双曲线上的三点,且x1<x2<0<x3,请直接写出y1,y2,y3的大小关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y=![]() (x>0)交于A(2,4),B(a,1),与x轴,y轴分别交于点C,D.
(x>0)交于A(2,4),B(a,1),与x轴,y轴分别交于点C,D.
(1)直接写出一次函数y=kx+b的表达式和反比例函数y=![]() (x>0)的表达式;
(x>0)的表达式;
(2)求证:AD=BC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为某城市部分街道示意图,四边形ABCD为正方形,点G在对角线BD上,GE⊥CD,GF⊥BC,AD=1500m,小敏行走的路线为B→A→G→E,小聪行走的路线为B→A→D→E→F.若小敏行走的路程为3100m,则小聪行走的路程为 m.
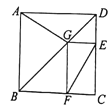
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形①、②在直线上,正方形③如图放置,若正方形①、②的面积分别为81 cm2和144 cm2,则正方形③的边长为( )

A. 225 cm B. 63 cm C. 50 cm D. 15 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个零件的形状如图所示,工人师傅按规定做得∠B=90°,
AB=3,BC=4,CD=12,AD=13,假如这是一块钢板,你能帮工人师傅计算一下这块钢板的面积吗?
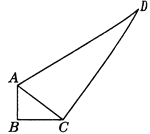
【答案】面积等于36
【解析】试题分析:利用勾股定理求AC,再利用勾股定理逆定理求∠ACB=90°,分别求![]() 的面积.
的面积.
试题解析:
![]() ∠B=90°,AB=3,BC=4,AC=
∠B=90°,AB=3,BC=4,AC=![]()
![]() =169,
=169,
所以∠ACD=90°,
![]() .
.
所以面积是36.
【题型】解答题
【结束】
22
【题目】如图,在所给正方形网格(每个小网格的边长是1)图中完成下列各题.
(1)格点△ABC(顶点均在格点上)的面积=_________;
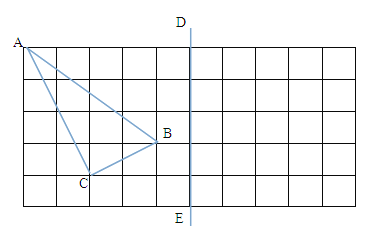
(2)画出格点△ABC关于直线DE对称的△A1B1C1;
(3)在DE上画出点P,使PB+PC最小,并求出这个最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,对角线AC,BD相交于O点,点P是线段AD上一动点(不与点D重合),PO的延长线交BC于Q点.
(1)求证:四边形PBQD为平行四边形.
(2)若AB=3cm,AD=4cm,P从点A出发.以1cm/s的速度向点D匀速运动.设点P的运动时间为ts,问:四边形PBQD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学在做作业时,遇到这样一道几何题:
已知:如图1,l1∥l2∥l3,点A、M、B分别在直线l1,l2,l3上,MC平分∠AMB,∠1=28°,∠2=70°.求:∠CMD的度数.
小明想了许久没有思路,就去请教好朋友小坚,小坚给了他如图2所示的提示:
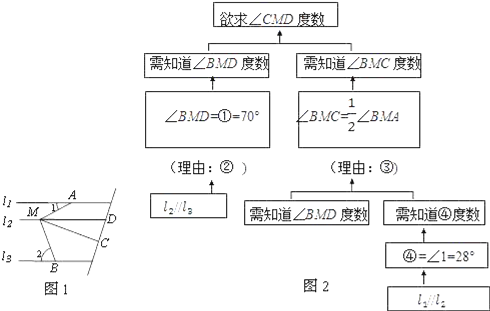
请问小坚的提示中①是∠ ,④是∠ .
理由②是: ;
理由③是: ;
∠CMD的度数是 °.
查看答案和解析>>
科目:初中数学 来源: 题型:
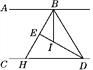
【题目】如图,已知BE平分∠ABD,DE平分∠BDC,且∠EBD+∠EDB=90°.
(1)试说明:AB∥CD;
(2)H是BE的延长线与直线CD的交点,BI平分∠HBD,写出∠EBI与∠BHD的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com