
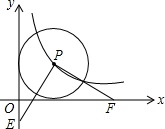
 如图,点P为反比例函数y=$\frac{1}{x}$(x>0)图象上一点,以点P为圆心作圆,且该圆恰与两坐标轴都相切.在y轴任取一点E,连接PE并过点P作直线PE的垂线与x轴交于点F,则线段OE与线段OF的长度可能满足的数量关系式是OF-OE=2或OE-OF=2或OF+OE=2.
如图,点P为反比例函数y=$\frac{1}{x}$(x>0)图象上一点,以点P为圆心作圆,且该圆恰与两坐标轴都相切.在y轴任取一点E,连接PE并过点P作直线PE的垂线与x轴交于点F,则线段OE与线段OF的长度可能满足的数量关系式是OF-OE=2或OE-OF=2或OF+OE=2. 分析 利用P点在双曲线y=$\frac{1}{x}$(x>0)图象上且以P为圆心的⊙P与两坐标轴都相切求出P点,再利用△BPE≌△APF分三种情况列出OE与OF之间的关系即可.
解答 解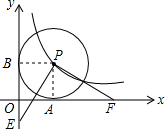 :∵点P在双曲线y=$\frac{1}{x}$(x>0)上,以P为圆心的⊙P与两坐标轴都相切,
:∵点P在双曲线y=$\frac{1}{x}$(x>0)上,以P为圆心的⊙P与两坐标轴都相切,
∴P( 1,1),
又∵PF⊥PE,
∴∠EPF=90°,
∵∠BPE+∠EPA=90°,
∴∠EPA+∠FPA=90°,
∴∠FPA=∠BPE,
在△BPE和△APF中
$\left\{\begin{array}{l}{∠EPB=∠FPA}\\{BP=AP}\\{∠EBP=∠PAF}\end{array}\right.$,
∴△BPE≌△APF,
∴AF=BE,
①当F在x轴的正半轴,且OF>1时,则有OF-OA=OB+OE,
即OF-1=1+OE,
∴OF-OE=2,
②当F在x轴的负半轴时,则有OF+OA=OE-OB,
即OF+1=OE-1,
∴OE-OF=2,
③当F在x轴的正半轴,且OF<1时,则有OA-OF=OE-OB,
即1-OF=OE-1,
∴OF+OE=2,
综上,线段OE与线段OF的长度可能满足的数量关系式是:OF-OE=2或OE-OF=2或OF+OE=2,
故答案为:OF-OE=2或OE-OF=2或OF+OE=2.
点评 此题主要考查了反比例函数与全等三角形的判定与性质的综合运用,同学们要熟练掌握反比例函数的性质,此题难度较大.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案 名题金卷系列答案
名题金卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a2=(b+c)(b-c) | B. | a:b:c=1:$\sqrt{3}$:2 | C. | a=32,b=42,c=52 | D. | a=5,b=12,c=13 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
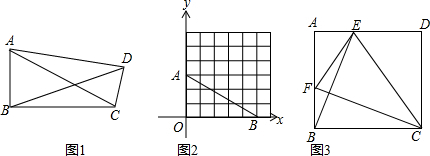
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
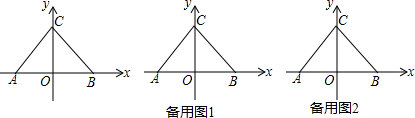
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com