
抛物线 与
与 轴交于点A,B,与y轴交于点C,其中点B的坐标为
轴交于点A,B,与y轴交于点C,其中点B的坐标为 .
.
(1)求抛物线对应的函数表达式;]
(2)将(1)中的抛物线沿对称轴向上平移,使其顶点M落在线段BC上,记该抛物线为G,求抛物线G所对应的函数表达式;
(3)将线段BC平移得到线段 (B的对应点为
(B的对应点为 ,C的对应点为
,C的对应点为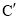 ),使其经过(2)中所得抛物线G的顶点M,且与抛物线G另有一个交点N,求点
),使其经过(2)中所得抛物线G的顶点M,且与抛物线G另有一个交点N,求点 到直线
到直线 的距离
的距离 的取值范围.
的取值范围.

(1)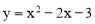 ;(2)
;(2) ;(3)
;(3)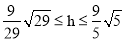 .
.
【解析】
试题分析:(1)根据曲线上点的坐标与方程的关系,将B 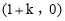 代入
代入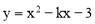 求出k即可.
求出k即可.
(2)应用待定系数法求出直线BC的解析式,将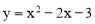 对称轴的
对称轴的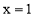 代入BC的解析式求得抛物线G的顶点坐标,从而得到抛物线G所对应的函数表达式.
代入BC的解析式求得抛物线G的顶点坐标,从而得到抛物线G所对应的函数表达式.
(3)连接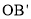 ,过点
,过点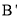 作
作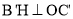 于点H,由
于点H,由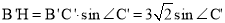 知当
知当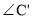 最大时h最大,当
最大时h最大,当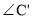 最小时h最小.,即当
最小时h最小.,即当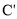 与M重合时,
与M重合时,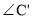 最大,h最大;当
最大,h最大;当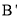 与M重合时,
与M重合时,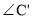 最小,h最小,据此求解即可.
最小,h最小,据此求解即可.
试题解析:(1)将B 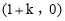 代入
代入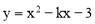 得
得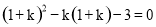 ,解得
,解得 .
.
∴抛物线对应的函数表达式为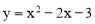 .
.
(2)由题意得,B(3,0),C( ).
).
∴直线BC的解析式为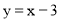 .
.
由(1)得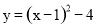 ,
,
∵将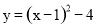 的图象向上平移时,横坐标不变,
的图象向上平移时,横坐标不变,
∴将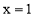 代入
代入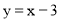 得
得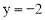 .
.
∴抛物线G的顶点坐标为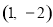 。
。
∴抛物线G所对应的函数表达式为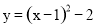 ,即
,即 .
.
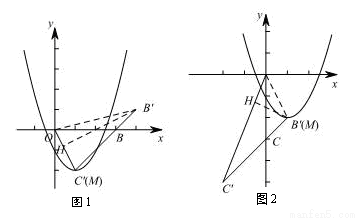
(3)如图1,连接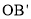 ,过点
,过点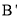 作
作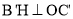 于点H,
于点H,
∵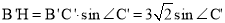 ,
,
∴当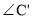 最大时h最大,当
最大时h最大,当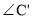 最小时h最小.
最小时h最小.
由图1可知当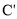 与M重合时,
与M重合时,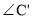 最大,h最大.
最大,h最大.
此时,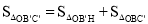 ,即
,即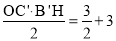 ,∴
,∴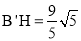 .
.
由图2可知当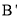 与M重合时,
与M重合时,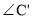 最小,h最小.
最小,h最小.
此时, ,即
,即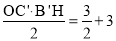 ,
,
此时, ,∴
,∴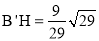 .
.
综上所述,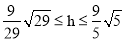 .
.
考点:1.二次函数综合题;2.平移的性质;3.待定系数法的应用;4.曲线上点的坐标与方程的关系;5.二次函数的性质;6.三角形的面积;7.转换思想的应用.


 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:初中数学 来源:2014年初中毕业升学考试(内蒙古呼和浩特卷)数学(解析版) 题型:解答题
如图,一艘海轮位于灯塔P的北偏东65 方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45
方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45 方向上的B处,这时,海轮所在的B处距离灯塔P有多远?(结果用非特殊角的三角函数及根式表示即可)
方向上的B处,这时,海轮所在的B处距离灯塔P有多远?(结果用非特殊角的三角函数及根式表示即可)

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(内蒙古包头、乌兰察布卷)数学(解析版) 题型:选择题
2013年我国GDP总值为56.9万亿元,增速达7.7%,将56.9万亿元用科学记数法表示为( )
A.56.9×1012元 B.5.69×1013元 C.5.69×1012元 D.0.569×1013元
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市西城区中考一模数学试卷(解析版) 题型:解答题
平面直角坐标系 中,一次函数
中,一次函数 和反比例函数
和反比例函数 的图象都经过点
的图象都经过点 .
.
(1)求 的值和一次函数的表达式;
的值和一次函数的表达式;
(2)点B在双曲线 上,且位于直线
上,且位于直线 的下方,若点B的横、纵坐标都是整数,直接写出点B的坐标.
的下方,若点B的横、纵坐标都是整数,直接写出点B的坐标.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市西城区中考一模数学试卷(解析版) 题型:填空题
如图,菱形ABCD中, ,DF⊥AB于点E,且DF=DC,连接FC,则∠ACF的度数为 度.
,DF⊥AB于点E,且DF=DC,连接FC,则∠ACF的度数为 度.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市燕山区中考一模数学试卷(解析版) 题型:解答题
如图,在平面直角坐标系中,点O坐标原点,直线l分别交x轴、y轴于A,B两点,OA<OB,且OA、OB的长分别是一元二次方程 的两根.
的两根.
(1)求直线AB的函数表达式;
(2)点P是y轴上的点,点Q第一象限内的点.若以A、B、P、Q为顶点的四边形是菱形,请直接写出Q的坐标.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市海淀区中考一模数学试卷(解析版) 题型:选择题
据教育部通报,2014年参加全国硕士研究生入学考试的人数约为1720000.数字1720000用科学记数法表示为( )
A. B.
B. C.
C.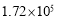 D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com