Question

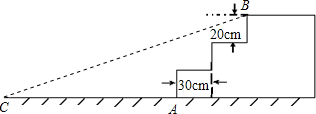
4．奥运会期间，某公园入口处原有三级台阶，为方便残疾人士，拟将台阶改为斜坡，每级台阶高为20cm，深为30cm．设台阶的起点为A，斜坡的起始点为C，现将斜坡的坡角∠BCA设计为12°，求AC的长度．（参考数据：tan12°=$\frac{3}{14}$）

Answer 1

分析 过B点作BD⊥CD，可得Rt△CBD，根据每级台阶高为20cm，可得BD=60cm，然后根据∠BCA=12°，利用三角函数的知识解直角三角形求出CD的长度，继而可求出AC的长度．

解答 解：过B点作BD⊥CD，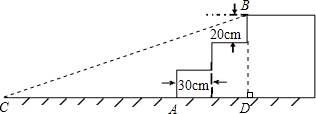
则△CBD为直角三角形，
∵tan∠BCA=tan12°=$\frac{BD}{CD}$=$\frac{3}{14}$，
∴$\frac{60}{CD}$=$\frac{3}{14}$，
∴CD=280，
∴AC=CD-60=220（cm）．
即AC的长度为220cm．

点评 本题考查了解直角三角线的应用，解答本题的关键是根据坡度构造直角三角形，利用三角函数的知识求解直角三角形．