
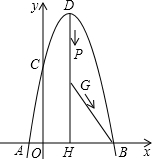
 ������y=-x2+��2m+3��x+5m+$\frac{5}{2}$��x�ύ��A��-1��0����B��x2��0�����㣬
������y=-x2+��2m+3��x+5m+$\frac{5}{2}$��x�ύ��A��-1��0����B��x2��0�����㣬���� ��1����A��������������߽���ʽ�����m��ֵ������������߽���ʽ��
��2����A��B���ڶԳ���Գƿ�֪QA+QC=QB+QC����֪��B��Q��C������һ������ʱ������������B��C��������ֱ��BC�Ľ���ʽ��ֱ��BC��Գ���Ľ��㼴Ϊ�����Q�㣻
��3����ͼ2�У�ȡG�䣨2��$\frac{9}{4}$������BG��=$\frac{15}{4}$������BG�䣬��DM��BG����M��GN��DM��N��������t=$\frac{DG}{5v}$+$\frac{BG}{3v}$=$\frac{1}{3v}$��$\frac{3}{5}$DG+BG�����ɡ�BHG��ס�DMG�䣬�Ƴ�$\frac{HG��}{MG��}$=$\frac{BG��}{DG��}$���Ƴ�MG��=$\frac{3}{5}$DG�䣬ͬ��֤��NG=$\frac{3}{5}$DG����������$\frac{1}{3v}$��$\frac{3}{5}$DG+BG������СֵֻҪ��$\frac{1}{3v}$��GN+BG������Сֵ�����ݴ��߶���̿�֪������G��G���غ�ʱ��$\frac{1}{3v}$��GN+BG����ֵ��С���ɴ˼��ɽ�����⣮
��� �⣺��1����A��-1��0������y=-x2+��2m+3��x+5m+$\frac{5}{2}$��0=-1-2m-3+5m+$\frac{5}{2}$�����m=$\frac{1}{2}$��
�������ߵĽ���ʽΪy=-x2+4x+5��
��2�����ڣ�
���ɣ���ͼ1�У���A��B���ڶԳ���Գƿ�֪QA+QC=QB+QC����֪��B��Q��C������һ������ʱ����������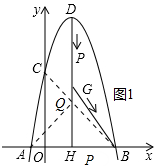
����������y=-x2+4x+5����y=0�õ�x=-1��5����x=0�õ�y=5��
��A��-1��0����
��B��5��0����C��0��5����
��ֱ��BC�Ľ���ʽΪy=-x+5��
�������ߵĶԳ���Ϊx=2��
��Q��2��3����
��3����ͼ2�У�ȡG�䣨2��$\frac{9}{4}$������BG��=$\frac{15}{4}$������BG�䣬��DM��BG����M��GN��DM��N��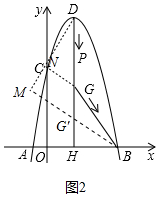
������t=$\frac{DG}{5v}$+$\frac{BG}{3v}$=$\frac{1}{3v}$��$\frac{3}{5}$DG+BG����
�ߡ�BHG��ס�DMG�䣬
��$\frac{HG��}{MG��}$=$\frac{BG��}{DG��}$��
��MG��=$\frac{3}{5}$DG�䣬ͬ��֤��NG=$\frac{3}{5}$DG��
������$\frac{1}{3v}$��$\frac{3}{5}$DG+BG������СֵֻҪ��$\frac{1}{3v}$��GN+BG������Сֵ��
���ݴ��߶���̿�֪������G��G���غ�ʱ��$\frac{1}{3v}$��GN+BG����ֵ��С��
��ʱG��2��$\frac{9}{4}$����
���� ���⿼����κ����ۺ��⡢����ϵ���������������εĵ��������ʡ���������֪ʶ������Ĺؼ���ѧ�����öԳƽ����Сֵ���⣬ѧ�ṹ�����������Σ����ô��߶���̣����������⣬�����п��������ͣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������y=ax2-x-$\frac{3}{2}$��x�������ύ�ڵ�A��3��0������OAΪ����x���Ϸ���������OABC���ӳ�CB���������ڵ�D������BDΪ��������������BDEF����a��ֵ�͵�E�����꣮
��ͼ��������y=ax2-x-$\frac{3}{2}$��x�������ύ�ڵ�A��3��0������OAΪ����x���Ϸ���������OABC���ӳ�CB���������ڵ�D������BDΪ��������������BDEF����a��ֵ�͵�E�����꣮�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com