
【题目】如图,以直线AB上一点O为端点作射线OC,使∠BOC=70°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°)
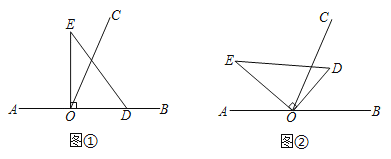
(1)如图①,若直角三角板DOE的一边OD放在射线OB上,则∠COE= °;
(2)如图②,把图①中直角三角板DOE绕点O逆时针方向以10°每秒的速度转动,求至少转多少秒能使OC恰好平分∠BOE?
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:初中数学 来源: 题型:
【题目】已知:线段AB=20cm.
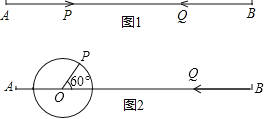
(1)如图1,点P沿线段AB自A点向B点以2厘米/秒运动,点Q沿线段BA自B点向A点以3厘米/秒运动,经过________秒,点P、Q两点能相遇.
(2)如图1,点P沿线段AB自A点向B点以2厘米/秒运动,同时点Q沿线段BA自B点向A点以3厘米/秒运动,问再经过几秒后P、Q相距5cm?
(3)如图2,AO=4cm,PO=2cm,∠POB=60°,点P绕着点O以60°/秒的速度逆时针旋转一周停止,同时点Q沿直线BA自B点向A点运动,假若点P、Q两点能相遇,求点Q运动的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
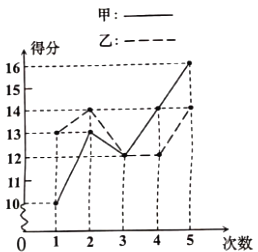
【题目】甲乙两人参加某项体育训练,近期五次测试成绩得分情况如图所示:
(1)分别求出两人得分的平均数;
(2)谁的方差较大?
(3)根据图表和(1)的计算,请你对甲、乙两人的训练成绩作出评价.
查看答案和解析>>
科目:初中数学 来源: 题型:
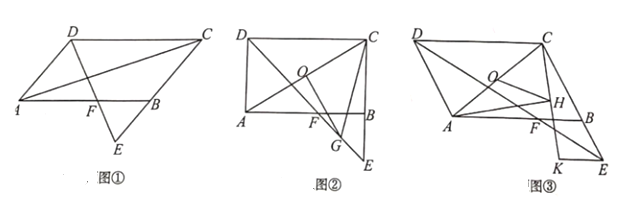
【题目】在ABCD中,∠ADC的平分线交直线BC于点E,交直线AB于点F.
(1)如图①,证明:BE=BF.
(2)如图②,若∠ADC=90°,O为AC的中点,G为EF的中点,试探究OG与AC的位置关系,并说明理由.
(3)如图③,若∠ADC=60°,过点E作DC的平行线,并在其上取一点K(与点F位于直线BC的同侧),使EK=BF,连接CK,H为CK的中点,试探究线段OH与HA之间的数量关系,并对结论给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,王老师布置如下任务:
如图1,△ABC中,BC>AB>AC,在BC边上取一点P,使∠APC=2∠ABC.
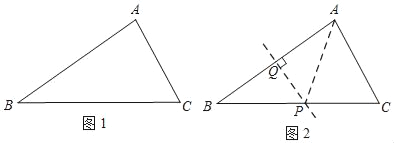
小路的作法如下,如图2:
①作AB边的垂直平分线,交BC于点P;
②连结AP.
所以,∠APC=2∠ABC.
小路的作图依据是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
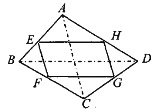
【题目】如图,四边形 ABCD 中,E、F、G、H 分别为各边的中点,顺次连 结 E、F、G、H,把四边形 EFGH 称为中点四边形.连结 AC、BD,容易证明:中点 四边形 EFGH 一定是平行四边形.
(1)如果改变原四边形 ABCD 的形状,那么中点四边形的形状也随之改变,通过探索 可以发现:当四边形 AB CD 的对角线满足 AC=BD 时,四边形 EFGH 为菱形;当四边形ABCD 的对角线满足 时,四边形 EFGH 为矩形;当四边形 ABCD 的对角线满足 时,四边形 EFGH 为正方形.
(2)试证明:S△AEH+S△CFG= ![]() S□ ABCD
S□ ABCD
(3)利用(2)的结论计算:如果四边形 ABCD 的面积为 2012, 那么中点四边形 EFGH 的面积是 (直接将结果填在 横线上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[ 问题提出 ]
一个边长为 ncm(n3)的正方体木块,在它的表面涂上颜色,然后切成边长为1cm的小正方体木块,没有涂上颜色的有多少块?只有一面涂上颜色的有多少块?有两面涂上颜色的有多少块?有三面涂上颜色的多少块?
[ 问题探究 ]
我们先从特殊的情况入手
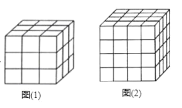
(1)当n=3时,如图(1)
没有涂色的:把这个正方形的表层“剥去”剩下的正方体,有1×1×1=1个小正方体;
一面涂色的:在面上,每个面上有1个,共有6个;
两面涂色的:在棱上,每个棱上有1个,共有12个;
三面涂色的:在顶点处,每个顶点处有1个,共有8个.
(2)当n=4时,如图(2)
没有涂色的:把这个正方形的表层“剥去”剩下的正方体,有2×2×2=8个小正方体:
一面涂色的:在面上,每个面上有4个,正方体共有 个面,因此一面涂色的共有 个;
两面涂色的:在棱上,每个棱上有2个,正方体共有 条棱,因此两面涂色的共有 个;
三面涂色的:在顶点处,每个顶点处有1个,正方体共有 个顶点,因此三面涂色的共有 个…
[ 问题解决 ]
一个边长为ncm(n3)的正方体木块,没有涂色的:把这个正方形的表层“剥去”剩下的正方体,有______个小正方体;一面涂色的:在面上,共有______个; 两面涂色的:在棱上,共有______个; 三面涂色的:在顶点处,共______个。
[ 问题应用 ]
一个大的正方体,在它的表面涂上颜色,然后把它切成棱长1cm的小正方体,发现有两面涂色的小正方体有96个,请你求出这个大正方体的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com