
【题目】甲乙两人参加某项体育训练,近期五次测试成绩得分情况如图所示:
(1)分别求出两人得分的平均数;
(2)谁的方差较大?
(3)根据图表和(1)的计算,请你对甲、乙两人的训练成绩作出评价.
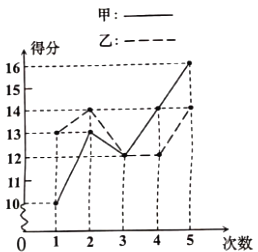
【答案】(1)13,13;(2)4,0.8;甲的方差大;(3)从平均数来看甲乙训练成绩一样,从图中可以看中,乙比较稳定,甲波动大.
【解析】
(1)根据图形,分别写出甲、乙两个人这五次的成绩,甲:10,13,12,14,16;乙:13,14,12,12,14;再根据平均数进行计算即可;
(2)由(1)利用和方差的公式进行计算即可
(3)根据方差和平均数的结果进行分析即可.
(1)两人得分的平均数:![]() 甲=
甲=![]() (10+13+12+14+16)=13,
(10+13+12+14+16)=13,
![]() 乙=
乙=![]() (13+14+12+12+14)=13,
(13+14+12+12+14)=13,
(2)方差:![]() 甲=
甲=![]() (9+0+1+1+9)=4,
(9+0+1+1+9)=4,
![]() 乙=
乙=![]() (0+1+1+1+1)=0.8,
(0+1+1+1+1)=0.8,
甲的方差大。
(3)从平均数来看甲乙训练成绩一样,从图中可以看中,乙比较稳定,甲波动大。


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,CD⊥AB,BE⊥AC,垂足分别为点D,点E,BE、CD相交于点O.∠1=∠2,则图中全等三角形共有( )
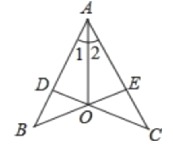
A. 4对B. 3对C. 2对D. 5对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=![]() AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②OE=OD;③BH=HF;④BC﹣CF=2HE;⑤AB=HF,其中正确的有( )
AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②OE=OD;③BH=HF;④BC﹣CF=2HE;⑤AB=HF,其中正确的有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD中,∠BAD=60°,点E、F分别是AB、AD上两个动点,若AE=DF,连接BF与DE相交于点G,连接CG,与BD相交于H。
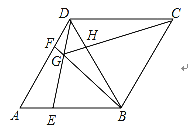
(1)求∠BGE的大小;(2)求证:GC平分∠BGD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2014贵州黔东南)黔东南州某超市计划购进一批甲、乙两种玩具,已知5件甲种玩具的进价与3件乙种玩具的进价的和为231元,2件甲种玩具的进价与3件乙种玩具的进价的和为141元.
(1)求每件甲种、乙种玩具的进价分别是多少元;
(2)如果购进甲种玩具有优惠,优惠方法是:购进甲种玩具超过20件,超出部分可以享受7折优惠.若购进x(x>0)件甲种玩具需要花费y元,请你求出y与x的函数关系式;
(3)在(2)的条件下,超市决定在甲、乙两种玩具中选购其中一种,且数量超过20件,请你帮助超市判断购进哪种玩具省钱.
查看答案和解析>>
科目:初中数学 来源: 题型:
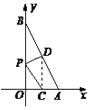
【题目】一次函数y=kx+b的图象与x、y轴分别交于点A(2,0),B(0,4).
(1)求该函数的解析式;
(2)O为坐标原点,设OA、AB的中点分别为C、D,P为OB上一动点,求PC+PD的最小值,并求取得最小值时P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以直线AB上一点O为端点作射线OC,使∠BOC=70°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°)
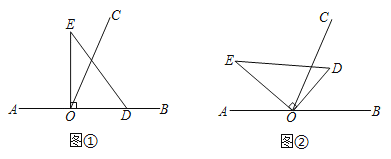
(1)如图①,若直角三角板DOE的一边OD放在射线OB上,则∠COE= °;
(2)如图②,把图①中直角三角板DOE绕点O逆时针方向以10°每秒的速度转动,求至少转多少秒能使OC恰好平分∠BOE?
查看答案和解析>>
科目:初中数学 来源: 题型:
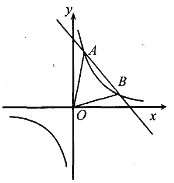
【题目】如图所示,在直角坐标系 xOy 中,一次函数![]() =
=![]() x+b(
x+b(![]() ≠0)的图象与反比例函数
≠0)的图象与反比例函数 ![]()
![]() 的图象交于A(1,4),B(2,m)两点.
的图象交于A(1,4),B(2,m)两点.
(1)试确定上述反比例函数和一次函数的表达式;
(2)求△AOB 的面积;
(3)当 x 的取值范围是 时,![]() x+b>
x+b>![]() (直接将结果填在横线上)
(直接将结果填在横线上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为美化校园,计划对面积为1800m2的区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且在独立完成面积为400 m2区域的绿化时,甲队比乙队少用4天.
(1)求甲、乙两工程队每天能完成绿化的面积分别是多少m2?
(2)若学校每天需付给甲队的绿化费用是0.4万元,乙队为0.25万元,要使这次的绿化总费用不超过8万元,至少应安排甲队工作多少天?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com